Cho ΔABC có AB=AC (góc A nhọn). Kẻ BH vuông góc với (H∈AC), kẻ CK vuông góc với AB(K∈AB); BH cắt CK tại I
A) CM: BH=CK
b)CM: ΔIBK=ΔICH. So sánh IK và IC
c) Gọi M là trung điểm của BC. CM: A,I,M thẳng hàng
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

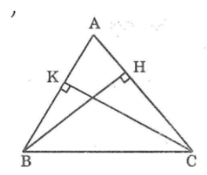
Tam giác ABH vuông tại H
⇒ ∠(ABH) +∠A =90o (tính chất tam giác vuông)
⇒∠(ABH) =90o - ∠A (1)
Tam giác ACK vuông tại K
⇒∠(ACK) +∠A =90o(tính chất tam giác vuông)
⇒∠(ACK) =90o-∠A (2)
từ (1) và (2) suy ra: ∠(ACK) =∠(ABH)

a: \(\widehat{ABH};\widehat{ACK}\) là các góc phụ với A
b: Vì \(\widehat{ABH}+\widehat{A}=90^0\)
mà \(\widehat{ACK}+\widehat{A}=90^0\)
nên \(\widehat{ABH}=\widehat{ACK}\)
\(\widehat{BIK}=\widehat{CIH}\)(hai góc đối đỉnh)

Ta có: ΔABC cân tại A
=> Góc B = góc C
=> AB = AC
Xét 2 ΔKBC và ΔHCB có
Góc B = góc C
BC chung
Góc BKC = góc BHC = 90o
=> ΔKBC = ΔHCB (c - g - c)
=> BK = HC
Mà AB = AC (cmt)
=> AK = AH (dpcm)

a: Xét ΔAHB vuông ạti H và ΔAKC vuông tại K có
AB=AC
góc BAH chung
=>ΔAHB=ΔAKC
=>AH=AK
b: Xét ΔAKI vuông tại K và ΔAHI vuông tại H co
AI chung
AK=AH
=>ΔAKI=ΔAHI
=>IH=IK
=>AI là trung trực của KI
c: góc EBC+góc ABC=90 độ
góc HBC+góc ACB=90 độ
góc ABC=góc ACB
=>góc EBC=góc HBC
=>BC là phân giác của góc HBE