Vẽ hình luôn hộ em với ạ
Cho tam giác ABC vuông tại A có AB = 3cm; BC = 5cm
a) Tính độ dài cạnh AC.
b) Trên tia đối của tia AB lấy điểm D sao cho AD = AB. Chứng minh Tam giác ABC = tam giác CDA.Từ đó=>tam giác BCD cân
c) Trên tia AC lấy điểm E sao cho AE=1/2 AC.Chứng minhDE đi qua trung điểmI của BC
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

a: Xét ΔCED vuông tại E và ΔCAB vuông tại A có
góc C chung
=>ΔCED đồng dạng với ΔCAB
b: BC=căn 3^2+4^2=5cm
Xét ΔABC có AD là phân giác
nên DB/AB=DC/AC
=>DB/3=DC/4=(DB+DC)/(3+4)=5/7
=>DC=20/7cm

a/ Xét △ABC vuông tại A:
\(BC^2=AB^2+AC^2\left(Pytago\right)\)
\(\Rightarrow BC=\sqrt{6^2+8^2}=10\left(cm\right)\)
- AM là đường trung tuyến của △ABC vuông tại A
\(\Rightarrow AM=MB=MC=\dfrac{BC}{2}\)
\(\Rightarrow AM=\dfrac{10}{2}=5\left(cm\right)\)
Vậy: \(AM=5cm\)
==========
b/ Tứ giác ABNC là hình chữ nhật vì:
- M là trung điểm của BC (gt) và AN (N đối xứng với A qua M)
⇒ ABNC là hình bình hành (Tứ giác có hai đường chéo cắt nhau tại trung điểm của mỗi đường là hình bình hành)
- ABNC có \(\hat{A}=90\text{°}\left(gt\right)\)
Vậy: ABNC là hình chữ nhật (Hình bình hành có một góc vuông là hình chữ nhật)
==========
c/ Ta có:
- \(IM=IK\left(gt\right);\hat{MIC}=90\text{°}\left(gt\right)\)
⇒AC là đường trung trực của MK \(\left(1\right)\)
- Mặt khác:
-Xét △CIM và △AIM có:
+ \(\hat{MIC}=\hat{MIA}=90\text{°}\left(gt\right)\)
+ \(IM\text{ }chung\)
+\(AM=MC\) (AM là trung tuyến của △ABC vuông tại A)
⇒ \(\text{△CIM = △AIM(c.h-c.g.v)}\)
\(\Rightarrow IA=IC\). Mà \(\hat{MIC}=90\text{°}\)
⇒MK là đường trung trực của AC \(\left(2\right)\)
Từ (1) và (2). Vậy: Tứ giác AMCK là hình thoi (Tứ giác có hai đường chéo là đường trung trực của nhau là hình thoi)

Áp dụng đl pytago vào tam giác vuông abc, ta có:
\(ab^2+ac^2=bc^2\)
\(6^2+8^2=bc^2\)
\(\Rightarrow bc=\sqrt{6^2+8^2}=10cm\)
ah=\(\dfrac{1}{2}bc=\dfrac{1}{2}10=5cm\)

Hình vẽ:
Xét \(\Delta AKC\)và \(\Delta AHB\)có:
\(BH=CK\left(gt\right)\)
\(\widehat{A}\)là góc chung
\(\widehat{AKC}=\widehat{AHB}\left(=90^0\right)\)
\(\Rightarrow\Delta AKC=\Delta AHB\left(ch.gn\right)\)
\(\Rightarrow AC=AB\)
\(\Rightarrow\Delta ABC\)cân tại A
Giả thiết: \(\Delta ABC,BH\perp AC\left(H\in AC\right),CK\perp AB\left(K\in AB\right),BH=CK\)
Kết luận: Chứng minh \(\Delta ABC\)cân?
Trả lời hơi muộn, have a nice day!
2 người ba đứa bé là bố đứa bé +1 đứa bé =2 người vì ba có thể viết là 3 nhưng tác giả lại cho là ba vậy bí ẩn ở chữ ba

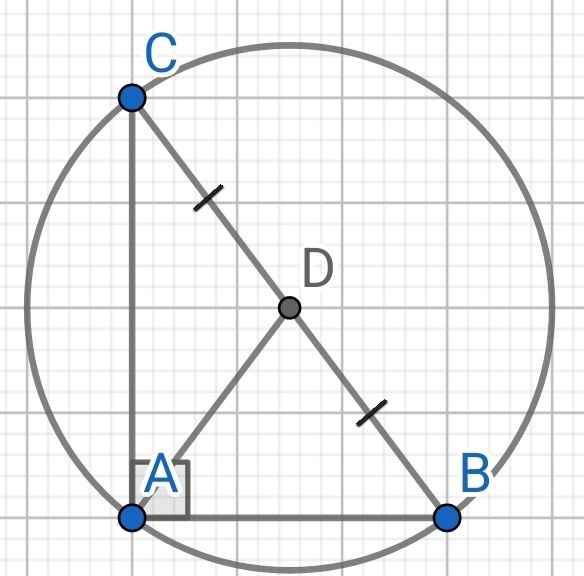 ∆ABC vuông tại A (gt)
∆ABC vuông tại A (gt)
BC² = AB² + AC² (Pytago)
= 6² + 8²
= 100
BC = 10 (cm)
Gọi D là trung điểm của BC
AD là đường trung tuyến ứng với cạnh huyền BC
AD = BD = CD = BC : 2 = 5 (cm)
Ba điểm A, B, C cùng nằm trên đường tròn tâm D, bán kính AD = 5 cm

a: BC=căn 3^2+4^2=5cm
AM là phân giác
=>MB/AB=MC/AC
=>MB/3=MC/4=(MB+MC)/(3+4)=5/7
=>MB=15/7cm; MC=20/7cm
b: Xét ΔBHM vuông tại H và ΔBAC vuông tại A có
góc B chung
=>ΔBHM đồng dạng với ΔBAC

không có đề vẽ hình bằng liềm tin à bạn: )
Cho tam giác ABC vuông tại A có AB = 3cm; BC = 5cm.