Cho hình thang ABCD \(\left(AB< CD\right)\) vuông tại A và D. Biết \(AD=2cm;BC=4cm\). Tính số đo góc của \(\widehat{B};\widehat{C}\)
K
Khách
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.
Những câu hỏi liên quan
CM
14 tháng 5 2019
. a) HS tự chứng minh
b) Kẻ đường cao AH, BK,chứng minh được DH = CK
Ta được H D = C D − A B 2 = 3 c m
Þ AH = 4cm Þ SABCD = 20cm2
22 tháng 9 2023
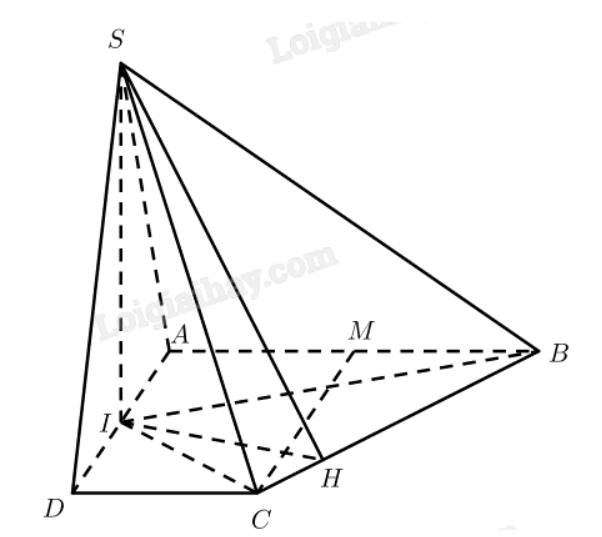
\(\left. \begin{array}{l}\left( {SBI} \right) \bot \left( {ABCD} \right)\\\left( {SCI} \right) \bot \left( {ABCD} \right)\\\left( {SBI} \right) \cap \left( {SCI} \right) = SI\end{array} \right\} \Rightarrow SI \bot \left( {ABCD} \right)\)
Kẻ \(IH \bot BC\left( {H \in BC} \right)\)
\(SI \bot \left( {ABCD} \right) \Rightarrow SI \bot BC\)
\( \Rightarrow BC \bot \left( {SIH} \right) \Rightarrow BC \bot SH\)
Vậy \(\widehat {AHI}\) là góc nhị diện \(\left[ {S,BC,A} \right]\)\( \Rightarrow \widehat {AHI} = {60^ \circ }\)
\(\begin{array}{l}{S_{ABC{\rm{D}}}} = \frac{1}{2}\left( {AB + C{\rm{D}}} \right).A{\rm{D}} = 3{a^2}\\AI = I{\rm{D}} = \frac{1}{2}A{\rm{D}} = a\\{S_{AIB}} = \frac{1}{2}AB.AI = {a^2},{S_{CI{\rm{D}}}} = \frac{1}{2}C{\rm{D}}.I{\rm{D}} = \frac{{{a^2}}}{2}\\ \Rightarrow {S_{BIC}} = {S_{ABC{\rm{D}}}} - {S_{AIB}} - {S_{CI{\rm{D}}}} = \frac{{3{a^2}}}{2}\end{array}\)
Gọi \(M\) là trung điểm của \(AB\)
\(\begin{array}{l} \Rightarrow BM = \frac{1}{2}AB = a,CM = AD = 2a \Rightarrow BC = \sqrt {B{M^2} + C{M^2}} = a\sqrt 5 \\ \Rightarrow IH = \frac{{2{{\rm{S}}_{BIC}}}}{{BC}} = \frac{{3a\sqrt 5 }}{5} \Rightarrow SI = IH.\tan \widehat {SHI} = \frac{{3a\sqrt {15} }}{5}\end{array}\)
\({V_{S.ABC{\rm{D}}}} = \frac{1}{3}{S_{ABC{\rm{D}}}}.SI = \frac{{3{a^3}\sqrt {15} }}{5}\)
21 tháng 8 2023
tham khảo:
a) Vì SA⊥(ABCD) nên SA⊥CD
Ta có: DC⊥AD;DC⊥SA nên DC⊥(SAD)
b) Vì SA⊥(ABCD) nên SA⊥CM
Ta có: AB = 2CD nên AM = CD. Suy ra AMCD là hình chữ nhật nên CM⊥AB
Mà CM⊥SA
Suy ra: CM⊥(SAB)
NV
Nguyễn Việt Lâm
Giáo viên
8 tháng 5 2023
B là khẳng định sai
\(\left\{{}\begin{matrix}SA\perp\left(ABCD\right)\Rightarrow SA\perp CD\\AD\perp CD\left(gt\right)\end{matrix}\right.\) \(\Rightarrow CD\perp\left(SAD\right)\)
\(CD=\left(SCD\right)\cap\left(BCD\right)\)
\(\Rightarrow\widehat{SDA}\) là góc giữa (SDC) và (BCD)
\(tan\widehat{SDA}=\dfrac{SA}{AD}=\sqrt{2}\Rightarrow\widehat{SDA}\approx54^044'\)
10 tháng 12 2023
ABCD là hình thang vuông tại A và D
=>\(S_{ABCD}=\dfrac{1}{2}\cdot AD\cdot\left(BA+CD\right)=\dfrac{1}{2}\cdot8\cdot\left(12+18\right)=4\cdot30=120\left(cm^2\right)\)
Diện tích tam giác ABD là:
\(S_{ABD}=\dfrac{1}{2}\cdot AB\cdot AD=\dfrac{1}{2}\cdot12\cdot8=4\cdot12=48\left(cm^2\right)\)
Ta có: \(S_{ABD}+S_{BDC}=S_{ABCD}\)
=>\(S_{BDC}+48=120\)
=>\(S_{BDC}=72\left(cm^2\right)\)
=>\(\dfrac{S_{BCD}}{S_{ABCD}}=\dfrac{72}{120}=\dfrac{3}{5}=60\%\)
OM
25 tháng 6 2017
Trường Huỳnh Đoàn
căn bậc 2 của 8 ( cm)
ai thấy đúng thì k nha
Từ B kẻ \(BE\perp DC;E\in DC\)
Dễ thấy ABED là HCN, có: \(BE=AD=2cm\)
\(\Delta BEC\) vuông tại E có \(BE=\dfrac{BC}{2}\) nên \(\Delta BEC\) bằng nửa tam giác đều Do đó: \(\widehat{C}=30^0;\widehat{CBE}=60^0\) Khi đó ta có: \(\widehat{ABC}=90^0+60^0=150^0\) Vậy hình thang \(ABCD\) có \(\widehat{B}=150^0;\widehat{C}=30^0\)