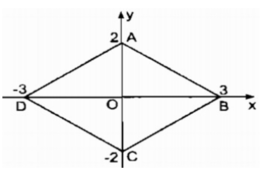
Cho tứ giác ABCD có A(0;1);B(0;4);C(6;4);D(4;-1).Gọi (d) là đường thẳng cắt AD;BC lần lượt tại M và N sao cho (d) chia tứ giác ABCD thành 2 phần có diện tích = nhau . biết đường thẳng (d) có dạng \(y=mx-\frac{5}{3}m\)(m khác 0)
a,tìm tọa độ giao điểm của M và N
b,Tìm tọa độ điểm Q trên mặt phẳng sao cho khoảng cách từ Q đến Ox bằng 2 lần khoảng cách từ Q đến Oy
AI TRÊN OLM BIẾT LÀM GIÚP MK NHÉ

a/AB=3;BC=4;AC=5 =>AB vuông góc với BC . Gỉa sử N(a;b)=>AN=a^2+(1-b)^2 ; BN=a^2+(4-b)^2 xong rồi áp dụng pytago vao tam giac ABN ta có: a^2+(1-b)2-a^2-(4-b)2 <=> b=24 => a=0=> N(0;4). Rồi cậu thay tọa độ của N vào pt đường thẳng d tính được m= -12/5
Gọi tọa độ của M(c;d) . cậu tìm pt đường thẳng AD là y=-1/2x +1
vì M vừa thuộc AD vừa thuộc d nên lập hệ : d=-1/2c+1 ; d= -12/5c-5/3 (cậu tự tìm c,d nhé)
A D C B M N
hình như bài này cậu đăng rồi đúng ko?