Cho Δ ABC vuông tại A có cạnh AB = 3 cm;AC = 4 cm. Tính diện tích của tam giác Δ ABC ?
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

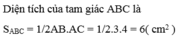

Áp dụng định lý Py – ta – go ta có: A C = ( B C 2 - A B 2 ) = ( 52 - 32 ) = 4 ( c m )
Δ ABC, AD là đường phân giác của góc BACˆ ( D ∈ BC )
Ta có: DB/DC = AB/AC hay DB/AB = DC/AC
Khi đó ta có: DB/DC = AB/AC ⇒ DB/( DB + DC ) = AB /( AB + AC )
hay DB/5 = 3/( 3 + 4) ⇒ DB = 15/7 cm; DC = 20/7 ( cm )
Chọn đáp án B.

Áp dụng định lý Py – ta – go ta có: A C = ( B C 2 - A B 2 ) = ( 5 2 - 3 2 ) = 4 ( c m )
Δ ABC, AD là đường phân giác của góc BACˆ ( D ∈ BC )
Ta có: DB/DC = AB/AC hay DB/AB = DC/AC
Khi đó ta có: DB/DC = AB/AC ⇒ DB/(DB + DC) = AB/(AB + AC)
hay DB/5 = 3/(3 + 4) ⇒ DB = 15/7 cm; DC = 20/7 ( cm )
Chọn đáp án B.

xét tam giác ABC vuông tại A ( gt)
\(AB^2+AC^2=BC^2\)
=> \(BC^2=AB^2+AC^2\)
= \(21^2+28^2=1225\)
=> BC = \(\sqrt{1225}=35\left(BC>0\right)\)
VẬY BC = 35 CM


Xét ΔABD và ΔEBD, ta có:
AB=BE ( gt)
Góc ABD= góc EBD ( Vì BD là tia phân giác của góc B)
BD chung
⇒ΔABD=ΔEBD(c-g-c)
b)Vì ΔABD=ΔEBD nên góc BAD= góc BED=90 độ( 2 cạnh tương ứng)
hay DE vuông góc với BC
c) Vì ΔABD=ΔEBD nên DA=DE ( 2 cạnh tương ứng)
Xét ΔADF và ΔEDC ta có:
góc FAD=góc CED(câu b)
AD=ED (cmt)
góc ADF=gócEDC( đối đỉnh)
⇒ΔADF=ΔEDC (g-c-g)
d,Xét ΔDAE và ΔDCF có:
DA=DC
Góc ADE=góc CDF (đối đỉnh)
DE=DF
⇒ΔDAE = ΔDCF (c-g-c)
⇒góc DAE=góc DCF (2 góc tương ứng)
MÀ 2 góc này ở vị trí SLT
⇒AE//CF
Đúg thì k
Mè sai cx k hộ nhen

a: BC=căn 21^2+28^2=35cm
BH=AB^2/BC=21^2/35=12,6cm
b: Xét ΔABH vuông tại H và ΔCBA vuông tại A có
góc B chung
=>ΔABH đồng dạng với ΔCBA

a: Xét ΔAHB vuông tại H và ΔAHC vuông tại H có
AB=AC
AH chung
=>ΔABH=ΔACH
b: góc DAH=góc HAC=góc DHA
=>ΔDAH cân tại D
=>góc DHB=góc DBH
=>DH=DB=DA
=>D là trung điểm của AB
=>DH=1/2AB

a)Xét tam giác ABC và tam giá HBA, có:
Góc B chung
Góc BAC = góc BHA
--> Tam giác ABC ~ Tam giác HBA