Cho tứ diện có các đỉnh là A(5;1;3), B(1;6;2), C(5;0;4), D(4;0;6). Tìm phương trình mặt phẳng (P) đi qua cạnh AB và song song với cạnh CD.
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

Ta có: AB → = (−4; 5; −1) và AC → = (0; −1; 1) suy ra n → = AB → ∧ n → = (4; 4; 4)
Do đó (ABC) có vecto pháp tuyến là n → = (4; 4; 4) hoặc n ' → = (1; 1; 1)
Suy ra phương trình của (ABC) là: (x – 5) + (y – 1) + (z – 3) = 0 hay x + y + z – 9 =0

Vecto pháp tuyến của mặt phẳng (ACD) vuông góc với hai vecto A C → = 0 ; - 1 ; 1 v à A D → = - 1 ; - 1 ; 3


Chọn D.
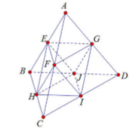
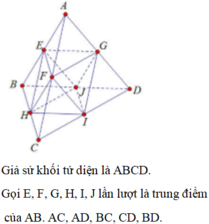
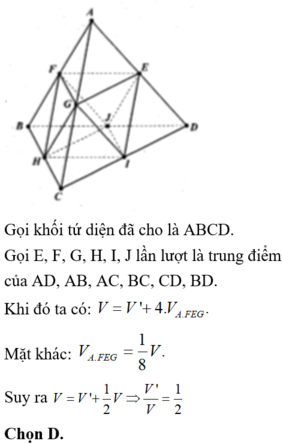
Giả sử khối tứ diện là ABCD. Gọi E, F, G, H, I, J lần lượt là trung điểm của AB. AC, AD, BC, CD, BD.
Ta có ![]()
![]()
Do đó ![]()
Vậy ![]()

Đáp án A
Gọi M,N,P,Q,H,R lần lượt là trung điểm của SA,SC,BC,AB,AC,SB
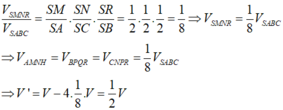

Đáp án A
Gọi M,N,P,Q,H,R lần lượt là trung điểm của SA,SC,BC,AB,AC,SB
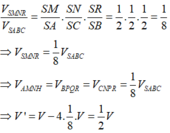

Chọn D.
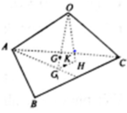
Gọi G1 là trọng tâm của tam giác ABC, H và K lần lượt là hình chiếu của O và G trên mặt phẳng (ABC). Khi đó
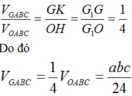

Gọi cạnh của tứ diện đều ABCD là a thì cạnh của hình bát diện đều (H) là a/2. Khi đó
![]()
Từ đó suy ra 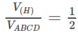
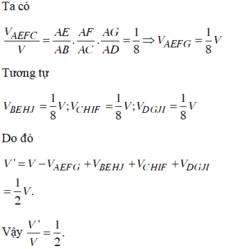
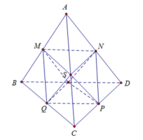

Chọn B