Cho đường thẳng ∆ có phương trình y = 4x – 2. Vectơ nào sau đây là vectơ pháp tuyến của ∆?
A. n 1 → = 1 ; 4
B. n 2 → = 4 ; − 1
C. n 3 → = 4 ; − 2
D. n 4 → = − 1 ; 4
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

ĐÁP ÁN C
Gọi u → ; n → lần lượt là vecto chỉ phương và vecto pháp tuyến của đường thẳng ∆ thì: u → . n → = 0
Ta có: 2. 3 + (-3).2 =0
Do đó, vecto n 3 → ( 3 ; 2 ) là vecto pháp tuyến của đường thẳng.

a) Phương trình tổng quát của đường thẳng\(\Delta \) đi qua điểm \(A\left( { - 1;{\rm{ }}2} \right)\) và có vectơ pháp tuyến \(\overrightarrow n = \left( {3{\rm{ }};{\rm{ }}2} \right).\)là: \(3\left( {x + 1} \right) + 2\left( {y - 2} \right) = 0 \Leftrightarrow 3x + 2y - 1 = 0\)
b) Do \(\Delta \) có vecto chỉ phương là \(\overrightarrow u = \left( { - 2{\rm{ }};{\rm{ 3}}} \right).\)nên vecto pháp tuyến của \(\Delta \) là \(\overrightarrow n = \left( {3{\rm{ }};{\rm{ }}2} \right).\)
Phương trình tổng quát của đường thẳng\(\Delta \) đi qua điểm \(A\left( { - 1;{\rm{ }}2} \right)\) và có vectơ pháp tuyến \(\overrightarrow n = \left( {3{\rm{ }};{\rm{ }}2} \right).\)là: \(3\left( {x + 1} \right) + 2\left( {y - 2} \right) = 0 \Leftrightarrow 3x + 2y - 1 = 0\)

Chọn D.
Đường thẳng đi qua A(-1; 2) nhận 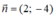 làm VTPT là:
làm VTPT là:
2.(x + 1) - 4.(y - 2) = 0 ⇔ 2x + 2 - 4y + 8 = 0 ⇔ 2x - 4y + 10 = 0 ⇔ x - 2y + 5 = 0

Vì Δ nhận vectơ ![]() làm vectơ pháp tuyến nên VTCP của Δ là
làm vectơ pháp tuyến nên VTCP của Δ là ![]() .
.
Vậy phương trình tham số của đường thẳng Δ là .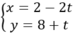
Chọn C.
ĐÁP ÁN B
Đường thẳng ∆ có phương trình y = 4x – 2 ⟺ 4x – y – 2 = 0 nên có một vectơ pháp tuyến là n → = 4 ; − 1