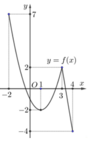
Cho hàm số y = f x liên tục và có đồ thị trên đoạn [−2;4] như hình vẽ bên. Tổng giá trị lớn nhất và nhỏ nhất của hàm số y = f x trên đoạn [−2;4] bằng
A. 5
B. 3
C. 0
D. -2
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

Đáp án C.
Quan sát đồ thị hàm số, ta thấy có hai điểm cực đại thuộc đoạn [-2; 3]

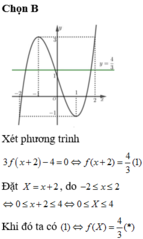
Vậy phương trình (1) có nghiệm trên đoạn [-2;2] khi và chỉ khi phương trình (*) có nghiệm trên đoạn [0;4]
Dựa vào hình vẽ ta nhận thấy trên đoạn [0;4] thì đường thẳng y = 4 3 cắt đồ thị hàm số đã cho đúng tại một điểm. Do đó phương trình (*) có đúng 1 nghiệm hay phương trình (1) có đúng một nghiệm.

![]()
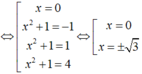
Các nghiệm trên đều là các nghiệm bội lẻ, do đó đều là cực trị của hàm số ![]()
Xét x = -1 ta có ![]()
từ đó ta có bảng xét dấu g’(x) như sau:
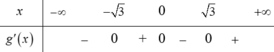
Dựa vào các đáp án ta thấy hàm số y = g(x) nghịch biến trên (0;1)
Chọn B
Chọn đáp án B
Có m a x [ - 2 ; 4 ] f x = f - 2 = 7
m i n [ - 2 ; 4 ] f x = f 4 = - 4
Tổng giá trị lớn nhất và giá trị nhỏ nhất bằng 3