Cho mặt phẳng đi qua điểm M(1; –3;4) và song song với mặt phẳng : 6x + 2y – z – 7 = 0. Phương trình mặt phẳng là :
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

Đáp án A
Phương trình mặt phẳng (α): 2(x - 1) + 3(y + 2) + 5(z - 4)=0<=> 2x + 3y + 5z - 16=0.

Đáp án C
Phương trình mặt phẳng qua M và song song với ( α ) là:
3(x-3)-(y+1)+2(z+2)=0 ⇔ 3x-y+2z-6=0

M’ đối xứng với M qua (α)
⇒ H là trung điểm MM’
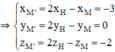
⇒ M’(-3; 0; -2).

H là trung điểm của MM’, suy ra x M ' = 2 x H - x M = −67/9
y M ' = 2 y H - y M = 29/9
z M ' = 2 z H - z M = −58/9
Vậy ta được ![]()

Đáp án B.
Phương pháp: Mặt phẳng ( α ) đi qua M(1; - 3;4) và nhận n β → = 6 ; - 5 ; 1 là 1 VTPT.
Cách giải: Mặt phẳng ( α ) đi qua M(1; - 3;4) và nhận n β → = 6 ; - 5 ; 1 là 1 VTPT nên có phương trình:
6(x - 1) - 5(y+3)+(z - 4)=0
→ 6x - 5y + z - 25 = 0
Đáp án B.
Phương pháp: Mặt phẳng ( α ) đi qua M(1; –3;4) và nhận n ( β ) → = ( 6 ; 2 - 1 ) là 1 VTPT.
Cách giải: Mặt phẳng ( α ) đi qua M(1; –3;4) và nhận n ( β ) → = ( 6 ; 2 - 1 ) là 1 VTPT nên có phương trình:
6(x– 1) + 2(y+3) – (z– 4) = 0 → 6x + 2y – z +4 = 0