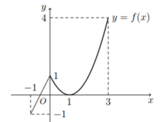
Cho hàm số f(x) liên tục trên [-1;3] và có đồ thị như hình vẽ bên. Gọi M, m lần lượt là giá trị lớn nhất và giá trị nhỏ nhất của hàm số y = f(x) trên [-1;3]. Tính M - m.
A. 3
B. 4
C. 5
D. 1
K
Khách
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.
Những câu hỏi liên quan
CM
3 tháng 11 2019
Quan sát bảng biến thiên ta thấy phương trình này có 2 nghiệm.
Chọn D
CM
10 tháng 2 2019
Chọn D
Dựa vào hình vẽ ta có : M = 3, m = -2. Do đó: M + m = 1
HT
18 tháng 4 2021
1/ \(\lim\limits_{x\rightarrow2^+}f\left(x\right)=\lim\limits_{x\rightarrow2^+}\left(x+1\right)=f\left(2\right)=3\)
\(\lim\limits_{x\rightarrow2^-}f\left(x\right)=\lim\limits_{x\rightarrow2^-}\dfrac{\left(x-2\right)\left(x-1\right)}{\left(x-2\right)\left(x^2+2x+4\right)}=\lim\limits_{x\rightarrow2^-}\dfrac{x-1}{x^2+2x+4}=\dfrac{1}{12}\)
\(\lim\limits_{x\rightarrow2^+}f\left(x\right)=f\left(2\right)\ne\lim\limits_{x\rightarrow2^-}f\left(x\right)\)
=> ham so gian doan tai x=2
2/ \(\lim\limits_{x\rightarrow2^-}f\left(x\right)=f\left(2\right)=2a-1\)
\(\lim\limits_{x\rightarrow2^+}f\left(x\right)=\lim\limits_{x\rightarrow2^+}\dfrac{3x-2-4}{\left(x-2\right)\left(\sqrt{3x-2}+2\right)}=\lim\limits_{x\rightarrow2^+}\dfrac{3}{\sqrt{3x-2}+2}=\dfrac{3}{4}\)
De ham so lien tuc tai x=2
\(\Leftrightarrow\lim\limits_{x\rightarrow2^-}f\left(x\right)=f\left(2\right)=\lim\limits_{x\rightarrow2^+}f\left(x\right)\Leftrightarrow2a-1=\dfrac{3}{4}\Leftrightarrow a=\dfrac{7}{8}\)
Chọn C
Quan sát đồ thị ta thấy hàm số y = f(x) đạt giá trị nhỏ nhất trên [-1;3] là -1 tại điểm x = =-1 và đạt giá trị lớn nhất trên[-1;3] là 4 tại điểm x = 3. Do đó M = 4, m = -1.
Giá trị M - m = 4 - (-1) = 5.