Có bao nhiêu giá trị của tham số m thuộc đoạn [-3;3] để hàm số f(x)= (m+1)x + m-2 đồng biến trên R
K
Khách
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

Những câu hỏi liên quan

CM
6 tháng 2 2019
Chọn B
Phương pháp: Sử dụng đạo hàm của hàm hợp để tính đạo hàm.


NV
Nguyễn Việt Lâm
Giáo viên
20 tháng 12 2020
ĐKXĐ: \(x\ge0\)
- Với \(x=0\) ko phải là nghiệm
- Với \(x>0\) chia 2 vế cho \(x\) ta được:
\(\dfrac{x^2+4}{x}+2-m=4\sqrt{\dfrac{x^2+4}{x}}\)
Đặt \(\sqrt{\dfrac{x^2+4}{x}}=t\ge2\)
\(\Rightarrow t^2-4t+2=m\)
Xét hàm \(f\left(t\right)=t^2-4t+2\) với \(t\ge2\)
\(\Rightarrow f\left(t\right)\ge f\left(2\right)=-2\Rightarrow m\ge-2\)
Có \(2018-\left(-2\right)+1=2021\) giá trị nguyên của m

AH
Akai Haruma
Giáo viên
19 tháng 12 2021
Lời giải:
Để $(m^2-4)x=m(m-2)$ có nghiệm duy nhất thì $m^2-4\neq 0$
$\Leftrightarrow (m-2)(m+2)\neq 0$
$\Leftrightarrow m\neq \pm 2$
Mà $m$ nguyên và $m\in [-5;5]$ nên $m\in\left\{-5; -4; -3; -1; 0; 1;3;4;5\right\}$


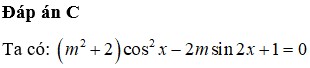
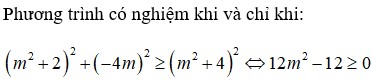
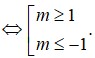
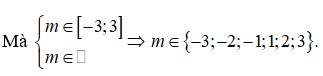
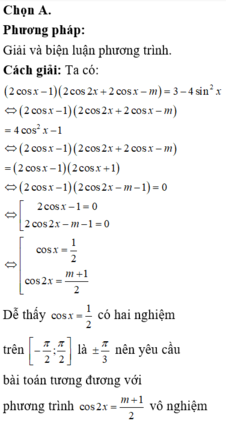



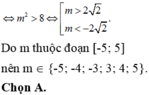

f(x) DB => m+1>0; m>-1
=>m={0;1;2;3}
co 4 giá trị nguyên của tham số m; f(x) đồng biến trên R