A) viết phương trình đường tròn (C) biết C có đường kính là AB với A(3;1), B(-5;3).
B) Cho đường tròn(C):(x+2)^2+(y-1)^2=16. viết phương trình tiếp tuyến của đường tròn (C), biết tiếp tuyến song song vs đthang d: 4x-3y-7=0
Giúp mk vs nhé :<<
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

Tọa độ tâm là:
\(\left\{{}\begin{matrix}x_O=\dfrac{1+7}{2}=4\\y_O=\dfrac{1+5}{2}=3\end{matrix}\right.\)
Vậy: Tọa độ tâm là O(4;3)
\(OA=\sqrt{\left(4-1\right)^2+\left(3-1\right)^2}=\sqrt{13}\)
Phương trình đường tròn là:
\(\left(x-4\right)^2+\left(y-3\right)^2=13\)

a: vecto AB=(7;1)
=>(d) có VTPT là (7;1)
Phương trình (d) là;
7(x-6)+1(y+2)=0
=>7x+y-40=0
b: Tọa độ K là:
x=(6-2)/2=2 và y=(4-2)/2=1
B(5;5); K(2;1)
vecto BK=(-3;-4)=(3;4)
=>VTPT là (-4;3)
Phương trình BK là:
-4(x-2)+3(y-1)=0
=>-4x+8+3y-3=0
=>-4x+3y+5=0
c: \(AC=\sqrt{\left(6+2\right)^2+\left(-2-4\right)^2}=10\)
Phương trình (C) là:
(x-5)^2+(y-5)^2=10^2=100

Gọi I là tâm đường tròn nhận AB là đường kính
⇒ I là trung điểm của AB ⇒ I (0; 0)
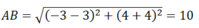
⇒ R = AB/2 = 5
Phương trình đường tròn (C) nhận AB là đường kính là:
x2 + y2 = 25

Đáp án: A
A(-1;2), B(1;4)
Gọi I là trung điểm của AB ⇒ I(0;3)
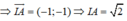
Đường tròn đường kính AB là đường tròn tâm I bán kính IA
⇒ (C): (x - 0 ) 2 + (y - 3 ) 2 = ( 2 ) 2 ⇔ x 2 + (y - 3 ) 2 = 2

Tọa độ trung điểm I của AB là: x = − 2 + 4 2 = 1 y = 1 + 1 2 = 1
Đường tròn có tâm I(1; 1) là trung điểm của AB và có bán kính R = I A = ( − 2 − 1 ) 2 + ( 1 − 1 ) 2 = 3 nên phương trình của đường tròn là:
x − 1 2 + y − 1 2 = 9 ⇔ x 2 + y 2 − 2 x − 2 y − 7 = 0
ĐÁP ÁN C

a) Viết phương trình tổng quát của AB và tính diện tích tam giác ABC
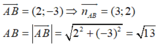
Phương trình tổng quát của AB là: 3(x - 1) + 2(y - 2) = 0 ⇔ 3x + 2y - 7 = 0
Kẻ CH ⊥ AB, (H ∈ AB)
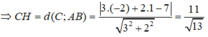
Diện tích tam giác ABC là:
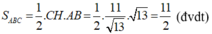
b) Viết phương trình đường tròn đường kính AB
Gọi I là trung điểm của AB
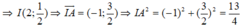
Đường tròn đường kính AB là đường tròn tâm I bán kính IA:
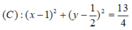

Gọi \(I\left(x_I;y_I\right)\) là trung điểm \(AB\) ( đồng thời là tâm đường tròn)
\(\left\{{}\begin{matrix}x_I=\dfrac{x_A+x_B}{2}=\dfrac{3+1}{2}=2\\y_I=\dfrac{y_A+y_B}{2}=\dfrac{3+5}{2}=4\end{matrix}\right.\)
\(\Rightarrow I\left(2;4\right)\)
\(\overrightarrow{AB}=\left(-2;2\right)\)\(\Rightarrow AB=\sqrt{\left(-2\right)^2+2^2}=2\sqrt{2}\)
Bán kính \(R=\dfrac{AB}{2}=\dfrac{2\sqrt{2}}{2}=\sqrt{2}\)
Vậy pt đường tròn \(\left(C\right):\left(x-2\right)^2+\left(y-4\right)^2=2\)
Gọi O(x; y) là tâm đường tròn
⇒O(2; 4)
⇒vectơ OA(1; -1)
⇒ R = |OA| = √2
Vậy phương trình đường tròn:
(x - 2)² + (y - 4)² = 2

a) Phương trình đường tròn \(\left( C \right)\) là: \({\left( {x + 2} \right)^2} + {\left( {y - 5} \right)^2} = 49\).
b) Bán kính đường tròn là: \(R = IA = \sqrt {{{\left( { - 2 - 1} \right)}^2} + {{\left( {2 - \left( { - 2} \right)} \right)}^2}} = 5\)
Phương trình đường tròn là: \({\left( {x - 1} \right)^2} + {\left( {y + 2} \right)^2} = 25\)
c) Gọi \(I\left( {a;b} \right)\) là trung điểm AB. Vậy tọa độ điểm I là: \(I\left( { - 2;1} \right)\)
Bán kính đường tròn là: \[R = IA = \sqrt {{{\left( { - 1 + 2} \right)}^2} + {{\left( { - 3 - 1} \right)}^2}} = \sqrt {17} \]
Phương trình đường tròn là: \({\left( {x + 2} \right)^2} + {\left( {y - 1} \right)^2} = 17\)
d) Bán kính đường tròn là: \(R = \frac{{\left| {1 + 2.3 + 3} \right|}}{{\sqrt {{1^2} + {2^2}} }} = 2\sqrt 5 \)
Phương trình đường tròn là: \({\left( {x - 1} \right)^2} + {\left( {y - 3} \right)^2} = 20\)
\(AB=\sqrt{\left(-5-3\right)^2+\left(3-1\right)^2}=2\sqrt{17}\)
\(\Rightarrow R=\frac{AB}{2}=\sqrt{17}\)
Gọi I là tâm đường tròn \(\Rightarrow\) I là trung điểm AB \(\Rightarrow I\left(-1;2\right)\)
Phương trình đường tròn: \(\left(x+1\right)^2+\left(y-2\right)^2=17\)
b/ Đường tròn tâm \(I\left(-2;1\right)\) bán kính \(R=4\)
Do tiếp tuyến song song với d nên pt tiếp tuyến d' có dạng \(4x-3y+c=0\)
Do d' là tiếp tuyến nên \(d\left(I;d'\right)=R\)
\(\Rightarrow\frac{\left|-2.4-3.1+c\right|}{\sqrt{4^2+\left(-3\right)^2}}=4\Leftrightarrow\left|c-11\right|=20\Rightarrow\left[{}\begin{matrix}c=31\\c=-9\end{matrix}\right.\)
Có 2 tiếp tuyến thỏa mãn: \(\left[{}\begin{matrix}4x-3y+31=0\\4x-3y-9=0\end{matrix}\right.\)