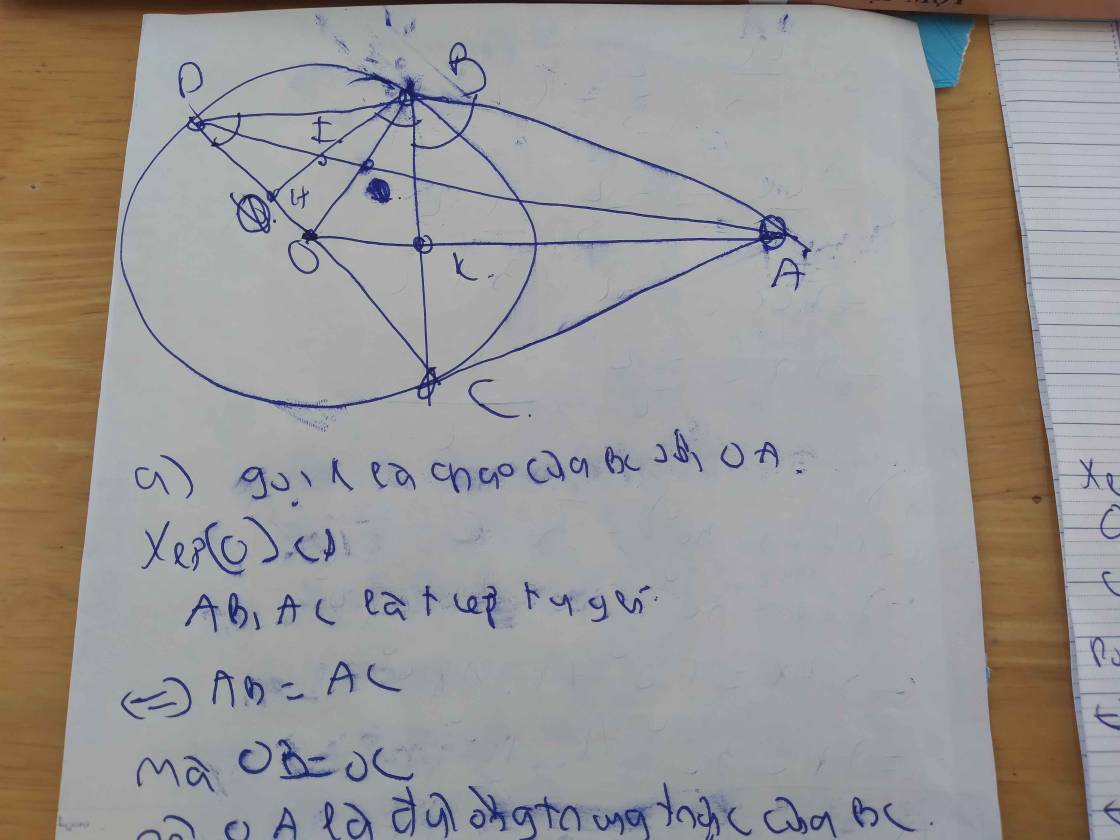
3. Cho đường tròn (O;3) và điểm A nằm ngoài đường tròn sao cho OA = 5.
Kẻ các tiếp tuyến AB, AC tới đường tròn (B, C là các tiếp điểm). Kẻ đường
kính CD của đường tròn.
a) Tính chu vi của tam giác BCD.
b) Kẻ BH vuông góc với CD tại H. Chứng minh rằng AD đi qua trung điểm
của BH
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

1: ΔABC cân tại A
=>AB=AC
mà OB=OC
nên AO là trung trực của BC
=>AD là đường kính của (O)
2: Xét (O) có
góc ACD là góc nội tiếp chắn nửa đường tròn
=>góc ACD=90 độ
3: ΔABC cân tại A
mà AH là đường cao
nên H là trung điểm của BC
=>HB=HC=BC/2=12cm
AH=căn AB^2-AH^2=16cm
ΔACD vuông tại C có CH là đường cao
nên AC^2=AH*AD
=>AD=20^2/16=25cm
=>R=12,5cm

1: \(AO=\sqrt{3^2+8^2}=\sqrt{73}\left(cm\right)\)
BC=2*R=6cm
\(CA=\sqrt{AB^2+BC^2}=\sqrt{8^2+6^2}=10\left(cm\right)\)
BD=6*8/10=4,8cm
2: Xét ΔBCE có
O là trung điểm của BC
OH//CE
=>H là trung điểm của BE
ΔOBE cân tại O
mà OH là trung tuyến
nên OH là phân giác của góc BOE
Xét ΔOBA và ΔOEA có
OB=OE
góc BOA=góc EOA
OA chung
=>ΔOBA=ΔOEA
=>góc OEA=90 độ
=>AE là tiếp tuyến của (O)

a) Gọi d là tiếp tuyến tại A của đường tròn (O) => d vuông góc OA => d vuông góc AB
Vì AB là đường kính của đường tròn (AB) nên d cũng là tiếp tuyến của (AB)
Vậy (O) và (AB) tiếp xúc nhau tại A (đpcm).
b) Gọi I là trung điểm đoạn AB => I là tâm của (AB) => ^ICA = ^IAC = ^OEA => IC // OE
Ta thấy OB = BI = IA = OA/3 => \(\frac{AI}{AO}=\frac{1}{3}\). Áp dụng ĐL Thales vào \(\Delta\)AEO có
\(\frac{AC}{AE}=\frac{AI}{AO}=\frac{1}{3}\) => AC = 1/3.AE (1)
Gọi OC,OD cắt đường tròn (O) cho trước lần lượt tại F,G. Khi đó DC // GF
Hay GF // AE. Mà GF và AE là các dây của đường tròn (O) nên (GE = (AF => ^EOG = ^AOF
Xét \(\Delta\)ODE và \(\Delta\)OCA: OD = OC, ^EOD = ^AOC (cmt), OE = OA => \(\Delta\)ODE = \(\Delta\)OCA (c.g.c)
=> ED = AC. Kết hợp với (1) suy ra AC = DE = AE/3 => AC = CD = DE (đpcm).

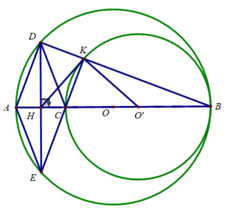
c) Ta có:
∠(CKB) = 90 0 (Góc nội tiếp chắn nửa đường tròn (O')) ⇒ CK ⊥ BD
∠(ADB) = 90 0 (Góc nội tiếp chắn nửa đường tròn (O)) ⇒ AD ⊥ BD
⇒ CK // AD
Lại có: CE // AD (Tứ giác ADCE là hình thoi)
⇒ C, E, K thẳng hàng

Xét ΔOBA vuông tại A có \(cosBOA=\dfrac{OA}{OB}=\dfrac{1}{2}\)
nên \(\widehat{BOA}=60^0\)
Xét ΔOAC có OA=OC và \(\widehat{AOC}=60^0\)
nên ΔOAC đều
=>\(sđ\stackrel\frown{AC}\left(nhỏ\right)=60^0\)
Số đo cung AC lớn là:
\(360-60=300^0\)