Trong không gian Oxyz, cho tứ giác ABCD, có A(1;5;3), AB→=(1;2;−6), AD→(−2;−4;3), tọa độ điểm I∈BD thỏa...
Đọc tiếp
Trong không gian Oxyz, cho tứ giác ABCD, có A(1;5;3), AB→=(1;2;−6), AD→(−2;−4;3), tọa độ điểm I∈BD thỏa mãn
K
Khách
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.
Những câu hỏi liên quan
CM
25 tháng 3 2018
Chọn đáp án C.
Ta có
Áp dụng công thức ta có:
V A B C D = 1 6 A B ⇀ . A C ⇀ . A D ⇀ = 1 2
NV
Nguyễn Việt Lâm
Giáo viên
14 tháng 1 2022
Không có mặt phẳng nào là mặt phẳng Oxyz cả nên chắc đề ko đúng. Giả sử nó là Oxy đi
Ý tưởng giải bài toán như sau:
- Viết phương trình mp trung trực (P) của đoạn AB
- Viết pt tham số đường thẳng d là giao của (P) và Oxy
- C thuộc d nên quy tọa độ C về 1 ẩn
- Tính độ dài AB=AC sẽ tìm được tọa độ C
- Viết phương trình mp trung trực (Q) của AC
- Viết pt tham số đường thẳng d1 là giao của (P) và (Q)
- D thuộc d1 => quy tọa độ D theo 1 ẩn, tính độ dài AD=AB => tọa độ D
Câu b thì giải hệ 3 tích vô hướng: SA.SB, SA.SC, SB.SC=0
CM
15 tháng 10 2019
Đáp án B.
Ta có:
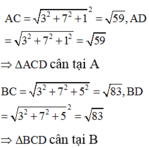
Từ đó gọi M là trung điểm của CD ta có 
Do đó chu vi ∆ A B M là
(vì AB không thay đổi), tức là khi M là trung điểm cuả CD hay M(0;1;-1)
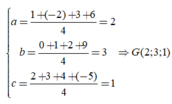
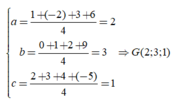
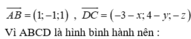
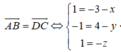
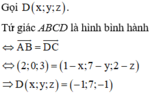
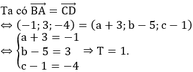
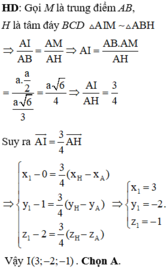
\(B\left(2;7;-3\right)\) ; \(D\left(-1;1;6\right)\)
\(I\left(x;y;z\right)\Rightarrow\left\{{}\begin{matrix}\overrightarrow{DI}=\left(x+1;y-1;z-6\right)\\\overrightarrow{DB}=\left(-3;-6;9\right)\end{matrix}\right.\)
\(\Rightarrow\left\{{}\begin{matrix}x+1=\frac{2}{3}.\left(-3\right)\\y-1=\frac{2}{3}.\left(-6\right)\\z-6=\frac{2}{3}.9\end{matrix}\right.\) \(\Rightarrow\left\{{}\begin{matrix}x=-3\\y=-3\\z=12\end{matrix}\right.\) \(\Rightarrow I\left(-3;-3;12\right)\)
thoa man DI/BD=2/3