Bài 1: Vẽ ( O;2cm). Vẽ đoạn thẳng OA=3 cm cắt đường tròn tại điểm B.Vẽ ( B ; 1 cm)
a/ Hãy cho biết vị trí điểm A đối với ( B; 1 cm ) và giải thích
b/ Hãy cho biết vị trí điểm O đối với ( B; 1 cm) và giải thích
K
Khách
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.
Những câu hỏi liên quan
18 tháng 7 2021
Bài 1:
Vì ∠AOC = ∠BOD (đối đỉnh)
Vì ∠AOC + ∠BOD = 140o (gt)
⇒ ∠AOC = ∠BOD = 140o/2 = 70o
Ta có: ∠AOC + ∠AOD = ∠COD (2 góc kề bù)
Thay số: 70o + ∠AOD = 180o
∠AOD = 180o - 70o
∠AOD = 110o
Vì ∠AOD = ∠BOC (đối đỉnh)
⇒ ∠BOC = 110o
Vậy ∠AOC = 70o
∠BOD = 70o
∠AOD = 110o
∠BOC = 110o
25 tháng 8 2021
Bài 2:
a: Ta có: Ox là tia phân giác của \(\widehat{mOn}\)
nên \(\widehat{mOx}=\widehat{nOx}=\dfrac{180^0}{2}=90^0\)
b: Ta có: Oy là tia phân giác của \(\widehat{mOx}\)
nên \(\widehat{yOx}=\dfrac{90^0}{2}=45^0\left(1\right)\)
Ta có: tia Ot là tia phân giác của \(\widehat{nOx}\)
nên \(\widehat{xOt}=\dfrac{90^0}{2}=45^0\left(2\right)\)
Từ \(\left(1\right),\left(2\right)\) suy ra \(\widehat{xOy}=\widehat{xOt}\)
KV
5 tháng 10 2023
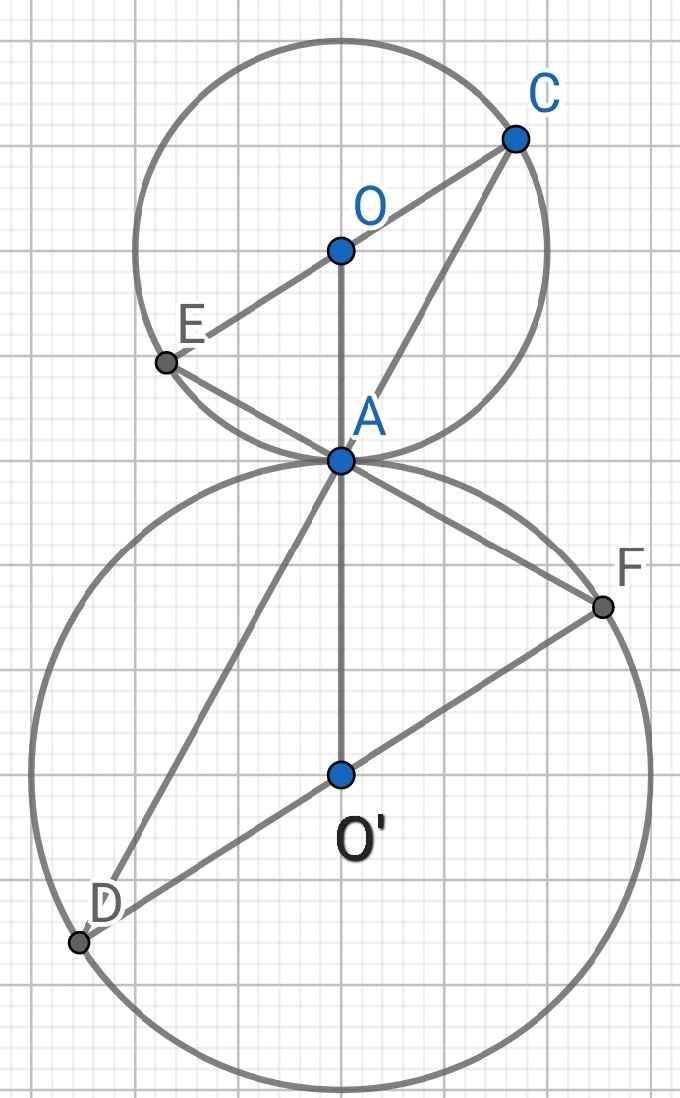
a) Đặt R là bán kính đường tròn tâm O
r là bán kính đường tròn tâm O'
Ta có:
OC = OA = R
∆OAC cân tại O
⇒ ∠OAC = ∠OCA
Mà ∠OAC = ∠O'AD (đối đỉnh)
⇒ ∠OCA = ∠O'AD (1)
Lại có:
O'A = OD = r
⇒ ∆O'AD cân tại O'
⇒ ∠O'AD = ∠O'DA (2)
Từ (1) và (2) suy ra ∠OCA = ∠O'DA
b) Sửa đề: chứng minh OC // O'D
Do ∠OCA = ∠O'DA (cmt)
Mà ∠OCA và ∠O'DA là hai góc so le trong
⇒ OC // O'D
c) Do CE là đường kính của đường tròn tâm O
A nằm trên đường tròn tâm O
⇒ ∆ACE vuông tại A
Hay AC ⊥ AE
19 tháng 9 2021
Vì thẳng hàng
Vì , ⇒ không phải trung điểm của
Mà không phải đường trung trực của
