Cho hàm số xác định và liên tục trên [-2;2] và có đồ thị là đường cong trong hình vẽ bên.
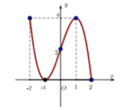
Hàm số f(x) đạt cực tiểu tại điểm
A. x = 1.
B. x = -2.
C. x = 2.
D. x = -1.
K
Khách
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.
Những câu hỏi liên quan
CM
9 tháng 1 2019
Dựa vào bảng biến thiên, ta có nhận xét như sau:
=> x = 0 là TCĐ.
không có TCN khi
x
→
+
∞
Vậy đồ thị hàm số có 2 đường tiệm cận. Chọn B.
CM
1 tháng 6 2019
Đáp án C
Các đường tiệm cận đứng là x = 1 ; x = − 1.
Tiệm cận ngang là
y
=
−
2
Vậy có tất cả 3 đường tiệm cận
CM
18 tháng 1 2019
Đáp án D.
Nhìn vào bảng ta thấy các đường tiệm cận là y = 1 ; x = − 1. Vậy đồ thị có 2 đường tiệm cận.
CM
7 tháng 9 2017
Dựa vào bảng biến thiên, ta có nhận xét sau
Hàm số nghịch biến trên khoảng - 3 ; - 2 v à - 2 ; - 1
=> A sai (sai chỗ dấu ∪ ).
Hàm số có giá trị cực đại y C Đ = - 2 => B sai
Hàm số đồng biến khoảng - ∞ ; - 3 và - 1 ; + ∞
=> C đúng. Chọn C.
Hàm số có điểm cực tiểu là -1 => D sai.
CM
17 tháng 12 2018
Đáp án C
Do lim x → + ∞ y = − ∞ ; lim x → − ∞ y = + ∞ nên đồ thị hàm số không có tiệm cận ngang. Do lim x → 0 − y = − 1 ⇒ x = 0 là tiệm cận đứng của đồ thị hàm số.
CM
16 tháng 8 2019
Chọn C
Từ bảng biến thiên ta thấy l i m x → + ∞ y = 5 ; l i m x → ∞ y = 3 đồ thị hàm số có hai đường tiệm cận ngang là y=5 và y=3. Và l i m x → 1 - y = - ∞ ⇒ x = 1 là đường tiệm cận đứng của đồ thị hàm số.
Vậy đồ thị hàm số có tất cả là ba đường tiệm cận
Chọn D.
Căn cứ vào đồ thị ta có
f'(x) < 0, ∀ x ∈ (-2;-1) và f'(x) > 0 , ∀ x ∈ (1;0)suy ra hàm số đạt cực tiểu tại x = -1.
f'(x) > 0 , ∀ x ∈ (0;1) và f'(x) < 0 , ∀ x ∈ (1;2) suy ra hàm số đạt cực đại tại x = 1.