Cho hàm số \(f\left(x\right)=ax^2+bx+c\) (a<0) có ĐT đi qua điểm (1;2).
Tìm tất cả các giá trị thực của tham số m để pt f(x)+m-2018=0 có nghiệm duy nhất.
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

f(0) = 1
\(\Rightarrow\) a.02 + b.0 + c = 1
\(\Rightarrow\) c = 1
Vậy hệ số a = 0; b = 0; c = 1
f(1) = 2
\(\Rightarrow\) a.12 + b.1 + c = 2
\(\Rightarrow\) a + b + c = 2
Vậy hệ số a = 1; b = 1; c = 1
f(2) = 4
\(\Rightarrow\) a.22 + b.2 + c = 4
\(\Rightarrow\) 4a + 2b + c = 4
Vậy hệ số a = 4; b = 2; c = 1
Chúc bn học tốt! (chắc vậy :D)

\(f\left(-1\right)=2\Rightarrow-a+b-c+d=2\\ f\left(0\right)=1\Rightarrow d=1\\ f\left(1\right)=7\Rightarrow a+b+c+d=7\\ f\left(\dfrac{1}{2}\right)=3\Rightarrow\dfrac{1}{8}a+\dfrac{1}{4}b+\dfrac{1}{2}c+d=3\)
\(d=1\Rightarrow-a+b-c=1;a+b+c=6\\ \Rightarrow2b=7\\ \Rightarrow b=\dfrac{7}{2}\\ \Rightarrow\dfrac{1}{8}a+\dfrac{7}{8}+\dfrac{1}{2}c=2\\ \Rightarrow\dfrac{1}{2}\left(\dfrac{1}{4}a+\dfrac{7}{4}+c\right)=2\\ \Rightarrow\dfrac{1}{4}a+\dfrac{7}{4}+c=4\\ \Rightarrow a+7+4c=16\\ \Rightarrow a+4c=9;a+c=6-\dfrac{7}{2}=\dfrac{5}{2}\\ \Rightarrow3c=\dfrac{13}{2}\Rightarrow c=\dfrac{13}{6}\\ \Rightarrow a=\dfrac{5}{2}-\dfrac{13}{6}=\dfrac{1}{3}\)
Vậy \(\left(a;b;c;d\right)=\left(\dfrac{1}{3};\dfrac{7}{2};\dfrac{13}{6};1\right)\)

Từ điều kiện đề bài \(\Rightarrow\left\{{}\begin{matrix}a+b+c=8\\-\dfrac{b}{2a}=2\\\dfrac{4ac-b^2}{4a}=9\end{matrix}\right.\Rightarrow f\left(x\right)=-x^2+4x+5\)
a. Không tồn tại m để \(3\left|f\left(x\right)\right|+m-5=0\) có 3 nghiệm phân biệt (nếu pt đã cho có 3 nghiệm thì 1 nghiệm trong đó luôn là nghiệm kép). Có 3 nghiệm thì được (khi đó \(\dfrac{5-m}{3}=9\Rightarrow m\))
b. \(2f\left(\left|x\right|\right)-7+5m=0\Leftrightarrow f\left(\left|x\right|\right)=\dfrac{-5m+7}{2}\) (1)
Đồ thì hàm \(y=f\left(\left|x\right|\right)\) (tạo ra bằng cách bỏ phần bên trái trục Oy và lấy đối xứng phần bên phải của đồ thị \(y=f\left(x\right)\) qua):
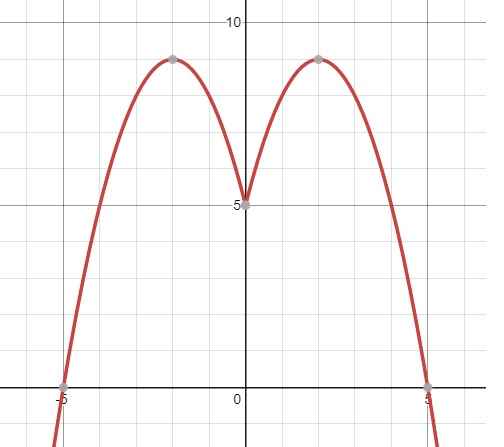
Từ đồ thị ta thấy (1) có 4 nghiệm pb khi:
\(5< \dfrac{-5m+7}{2}< 9\) \(\Rightarrow-\dfrac{11}{5}< m< -\dfrac{3}{5}\)

Ta có: f(0) = a.02 + b.0 + c = 2
=> c = 2
f(1) = a.12 + b.1 + c = 1
=> a + b + c = 1 => a + b = 1 - c = 1 - 2 = -1 (1)
f(-2) = a.(-2)2 + b.(-2) + c = 2
=> 4a - 2b = 2 - c = 2 - 2 = 0
=> 2a - b = 0 (2)
Từ (1) và (2) cộng vế theo vế:
(a + b) + (2a - b) = -1
=> 3a = -1
=> a = -1/3
=> b = -1 - a = -1 + 1/3 = -2/3
Vậy ....

vì đồ thị hàm số đi qua điểm \(A\left(-1;\frac{5}{2}\right)\) nên tọa độ của A thỏa mãn phương trình sau: \(\frac{a+b}{-2}=\frac{5}{2}\Rightarrow a+b=-5\)(*)
ta tính y' có:
\(y'=\frac{\left(2ax-b\right)\left(x-1\right)-\left(ax^2-bx\right)}{\left(x-1\right)^2}=\frac{2ax^2-2ax-bx+b-ax^2+bx}{\left(x-1\right)^2}=\frac{ax^2-2ax+b}{\left(x-1\right)^2}\)
vì hệ số góc của tiếp tuyến tại điểm O(0;0) bằng 3 nên \(y'\left(O\right)=\frac{b}{\left(0-1\right)^2}=-3\Rightarrow b=-3\)
thay b=-3 vào (*) ta tìm được a=-2
vậy a=-2;b=-3

\(\lim\limits_{x\rightarrow0}\dfrac{\sqrt[3]{ax+1}-\sqrt[]{1-bx}}{x}=\lim\limits_{x\rightarrow0}\dfrac{\dfrac{ax}{\sqrt[3]{\left(ax+1\right)^2}+\sqrt[3]{ax+1}+1}+\dfrac{bx}{1+\sqrt[]{1-bx}}}{x}\)
\(=\lim\limits_{x\rightarrow0}\left(\dfrac{a}{\sqrt[3]{\left(ax+1\right)^2}+\sqrt[3]{ax+1}+1}+\dfrac{b}{1+\sqrt[]{1-bx}}\right)=\dfrac{a}{3}+\dfrac{b}{2}\)
Hàm liên tục tại \(x=0\) khi:
\(\dfrac{a}{3}+\dfrac{b}{2}=3a-5b-1\Leftrightarrow8a-11b=3\)
Đề là đồ thị có đỉnh là \(\left(1;2\right)\) thì hợp lí hơn
\(f\left(x\right)+m-2018=0\)
\(\Leftrightarrow f\left(x\right)=2018-m\) là phương trình hoành độ giao điểm của hai đồ thị \(y=m-2018;y=f\left(x\right)\)
Phương trình \(f\left(x\right)+m-2018=0\) có nghiệm duy nhất khi \(2018-m=2\Leftrightarrow m=2016\)