Trong không gian Oxyz cho A(4;-2;6), B(2;4;2), M sao cho nhỏ nhất. Tọa độ của M bằng
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

Đáp án D
Ba điểm A, B, M thẳng hàng khi và chỉ khi hai vecto AB ⇀ ; AM → cùng phương
Ta có: ![]()
Do đó, ba điểm A, B, M4 thẳng hàng hay điểm M4 nằm trên đường thẳng AB.

Đáp án D.
Phương pháp: Viết phương trình mặt phẳng (ABC) dạng đoạn chắn.
Cách giải: Phương trình mặt phẳng (ABC):
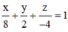
![]()

Đáp án D.
Phương pháp: Viết phương trình mặt phẳng (ABC) dạng đoạn chắn.
Cách giải: Phương trình mặt phẳng (ABC):
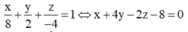

Ta biết rằng a → và b → cùng phương khi và chỉ khi a → = k b → với k là một số thực. Theo giả thiết ta có: b → = ( x 0 ; y 0 ; z 0 ) với x 0 = 2. Ta suy ra k = 1/2 nghĩa là l = x 0 /2
Do đó: −3 = y 0 /2 nên y 0 = -6
4 = z 0 /2 nên z 0 = 8
Vậy ta có b → = (2; −6; 8)

Tâm mặt cầu là trung điểm đoạn AB là I(2;-1;5). Bán kính mặt cầu là R = A B 2 = 3
Vậy phương trình mặt cầu x - 2 2 + y + 1 2 + z - 5 2 = 9
Chọn đáp án B.
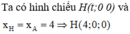
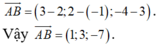
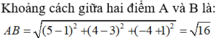
Chọn B
Gọi I là trung điểm AB => I(3;1;4). Gọi H là hình chiếu của I xuống mặt phẳng α .
Ta có
Do IA không đổi nên M A → . M B → nhỏ nhất khi MI nhỏ nhất .
Gọi ∆ là đường thẳng đi qua I và vuông góc với mặt phẳng α . Khi đó ∆ nhận
Do đó ∆ có phương trình