Cho hàm số f(x) xác định trên và thỏa mãn:
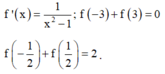
Tính giá trị của biểu thức P = f(0) + f(4)
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

Chọn C.
Ta có f ' x + 2 f x = 0 ⇔ f ' x = - 2 f x ⇔ f ' x f x = - 2 d o f x > 0
Lấy tích phân hai vế, ta được
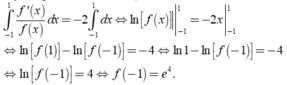

Đáp án D
f x = 2 x − 1 x + 1 f ' x = 2.1 − − 1 .1 x + 1 2 = 3 x + 1 2

Đáp án D
Ta có y ' = f 1 - x + 2018 x + 2019 ' = 1 - x ' . f ' 1 - x + 2018 = - f ' 1 - x + 2018
= - x 3 - x . g 1 - x - 2018 + 2018 = - x 3 - x . g 1 - x mà g 1 - x < 0 ; ∀ x ∈ ℝ
Nên y ' < 0 ⇔ - x 3 - x . g 1 - x < 0 ⇔ x 3 - x . g 1 - x > 0 ⇔ x 3 - x < 0 ⇔ [ x > 3 x < 0
Khi đó, hàm số y = f 1 - x + 2018 x + 2019 nghịch biến trên khoảng 3 ; + ∞

Đáp án A
Từ bảng biến thiên của hàm số y=f(x), suy ra bảng biến thiên của hàm số y = f ( x ) là
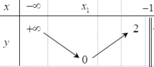

Dựa vào bảng biến thiên, ta suy ra hàm số có 4 điểm cực trị.

Đáp án A

Ta có:
![]()
⇒ f x 5 + 4 x + 3 = 2 x + 1 ⇒ ∫ - 1 1 5 x 4 + 4 . f x 5 + 4 x + 3 d x = ∫ - 1 1 5 x 4 + 4 . ( 2 x + 1 ) d x ⇔ ∫ - 2 8 f ( t ) d t = ∫ - 1 1 ( 10 x 5 + 5 x 4 + 8 x + 4 ) d x

Đáp án A
Vì hàm số không xác định tại x=-1 nên hàm số đồng biến trên ( - ∞ ; - 1 ) ; ( - 1 ; 1 ) .
Đáp án C