Trong không gian với hệ trục tọa độ Oxyz, cho các điểm A ( 1;2;3 ) và B ( 3;4;1 ) . Đặt P = M A → + M B ↔ trong đó M x 0 , y 0 z 0 là một điểm nằm trên (Oxy) thỏa mãn P m i n . Khi đó x 0 + y 0 + z 0 =
A. 4
B. 7 2
C. 5
D. 1
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.
. Tìm tọa độ điểm A.
Chọn B.
Gọi B, C, D lần lượt là hình chiếu của A lên các trục Ox , Oy , Oz ⇒ B ( 1 ; 0 ; 0 ) C ( 0 ; - 1 ; 0 ) D ( 0 ; 0 ; 2 )
Suy ra phương trình mặt phẳng ( Q ) : x 1 + y - 1 + z 2 = 1 ⇔ 2 x - y + z - 2 = 0 .
Đáp án C.
Hình chiếu của A(1 ;2 ;3) lên trục Ox là M(1;0;0)
Hình chiếu của A(1 ;2 ;3) lên trục Oy là N(0;2;0)
Hình chiếu của A(1 ;2 ;3) lên trục Ox là P(0;0;3)
Phương trình mặt phẳng (P) cần tìm là:
Chọn B.
Phương pháp: Kinh nghiệm: Chiếu lên trục, mặt phẳng đặc biệt thì thiếu gì thì cho đấy bằng 0.
Sau đó dùng phương trình mặt phẳng theo đoạn chắn để viết.
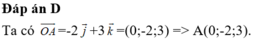
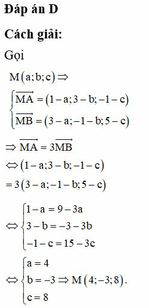
P = M A → + M B ↔ = 2 M I → với I ( 2;3;2 ) là trung điểm của AB
Vậy P m i n ứng với M là hình chiếu của I nên ( Oxy ) nên M ( 2;3;0 )
Vậy x 0 + y 0 + z 0 = 5
Đáp án cần chọn là C