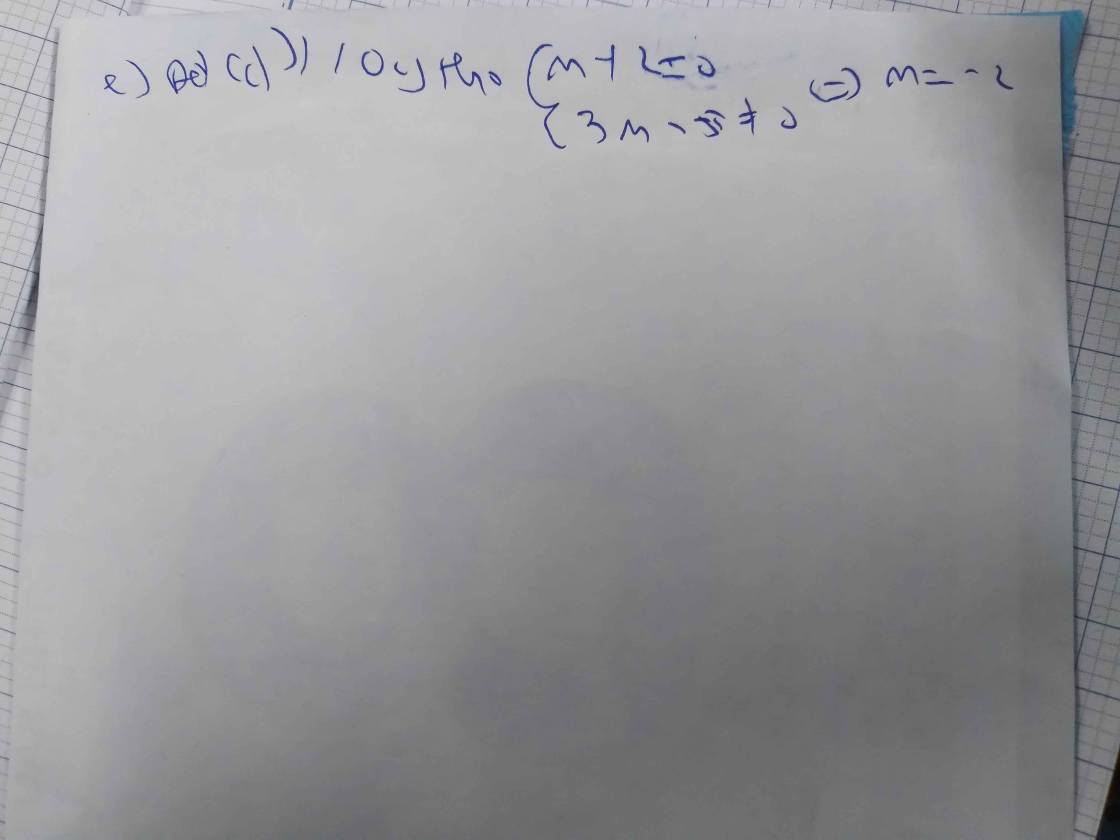- tim m de ham so y=\(\frac{x-m^2+m}{x-1}\) dat GTNN trong [0;1] = -2
K
Khách
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.
NM
0
Những câu hỏi liên quan
NM
0
TN
1 tháng 12 2017
Hàm số y = (m-1 )x +2 có phần hệ số a = m-1 , b = 2
Hàm số y = 3x +1 có phần hệ số a' = 3 , b' = 1
Để hàm số y = ( m -1)x +2 song song với hàm số y = x+3 thì
\(\left\{{}\begin{matrix}a=a'\\b\ne b'\end{matrix}\right.\Rightarrow m-1=3\Rightarrow m=4\)
Vậy...
b, Để đồ thị đi qua điểm M(2;-2) \(\Leftrightarrow-2=\left(m-1\right).2+2\)
\(\Leftrightarrow2m-2+2=-2\)
\(\Leftrightarrow m=-1\)
DP
1
14 tháng 6 2022
a Để đây là hàm số bậc nhất thì \(\dfrac{m-2}{m+2}< >0\)
hay \(m\notin\left\{2;-2\right\}\)
b: Để hàm số đồng biến thì 5-2m>0
=>2m<5
hay m<5/2
15 tháng 1 2022
a; Thay x=2 và y=-1 vào y=(2m+1)x, ta được:
4m+2=-1
=>4m=-3
hay m=-3/4
2 tháng 9 2020
\(y=\left(m-1\right)x\)
\(M\left(-1;2\right)\Rightarrow x=-1;y=2\)
\(2=\left(m-1\right)\cdot-1\)
\(2=-m+1\)
\(1=-m\)
\(m=-1\)
b.
\(y=\left(m-1\right)x\)
\(y=\left(-1-1\right)x\)
\(y=-2x\)