viết phương trình tổng quát của đường thẳng đi qua điểm M(\(\sqrt{2}\);1) và vuông góc với đường thẳng có phương trình (\(\sqrt{2}+1\))x+(\(\sqrt{2}\)-1)y+1 = 0
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.


5:
Gọi (d): y=ax+b là phương trình cần tìm
Theo đề, ta có hệ:
3a+b=-1 và 2a+b=3
=>a=-4 và b=11
=>y=-4x+11
4:
vecto BC=(1;-1)
=>AH có VTPT là (1;-1)
Phương trình AH là:
1(x-1)+(-1)(y+3)=0
=>x-1-y-3=0
=>x-y-4=0

\(\overrightarrow{PQ}=(-4;-2)=2(2;1)\)
a) Đường thẳng qua A(3;2) song song với PQ nhận \(\overrightarrow{PQ}=(-4;-2)=2(2;1)\) làm VTCP nên có pt
\(\dfrac{x-3}{2}=\dfrac{y-2}{1}\Leftrightarrow x-2y+1=0\)
b) Đường thẳng trung trực của PQ qua trung điểm của PQ là M(2;-1) và nhận \(\overrightarrow{PQ}=(-4;-2)=2(2;1)\)làm VTPT nên có pt
\(2(x-2)+(y+1)=0\Leftrightarrow 2x+y-3=0\)

a: vecto AB=(-1;6)
=>VTPT là (6;1)
Phương trình tham số là;
x=1-t và y=-2+6t
b: PTTQ là:
6(x-1)+1(y+2)=0
=>6x-6+y+2=0
=>6x+y-4=0

\(\Delta\left\{{}\begin{matrix}quaM\left(-2;3\right)\\VTCP=\overrightarrow{u}=\overrightarrow{MN}=\left(6;-2\right)\end{matrix}\right.\)
\(\Rightarrow\overrightarrow{VTPT}=\overrightarrow{n}=\left(2;6\right)\)
\(PTTQ\) của \(\Delta:a\left(x-x_o\right)+b\left(y-y_o\right)=0\)
\(\Leftrightarrow2\left(x+2\right)+6\left(y-3\right)=0\)
\(\Leftrightarrow2x+4+6y-18=0\)
\(\Leftrightarrow2x+6y-14=0\)
Vậy PTTQ của đường thẳng \(\Delta\) là : \(2x+6y-14=0\)
Ta có:
Vecto MN = (6; -2) = (3; -1) là vec tơ chỉ phương của (MN)
⇒ Vec tơ pháp tuyến của (MN) là n = (2; 6) = (1; 3)
Phương trình tổng quát của (MN):
(MN): 1.(x + 2) + 3(y - 3) = 0
⇔ x + 7 + 3y - 9 = 0
⇔ x + 3y - 7 = 0

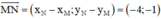
Đường thẳng MN nhận 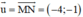 là 1 vtcp
là 1 vtcp
⇒ MN nhận 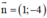 là 1 vtpt
là 1 vtpt
Mà M(4; 0) thuộc đường thẳng MN
⇒ Phương trình đường thẳng MN: 1(x - 4) – 4(y - 0) = 0 hay x – 4y – 4 = 0.
Gọi đt cần tìm là (d)
(d) vuông góc với đt có pt \(\left(\sqrt{2}+1\right)x+\left(\sqrt{2}-1\right)y+1=0\left(1\right)\) => VTPT của (1) là VTCP của (d)
(d) đi qua \(M\left(\sqrt{2};1\right)\) ; 1 VTCP: \(\left(\sqrt{2}+1;\sqrt{2}-1\right)\) => VTPT \(\left(-\sqrt{2}+1;\sqrt{2}+1\right)\)
\(\Rightarrow\left(d\right):\left(-\sqrt{2}+1\right)\left(x-\sqrt{2}\right)+\left(\sqrt{2}+1\right)\left(y-1\right)=0\)
\(\Leftrightarrow\left(-\sqrt{2}+1\right)x+2-\sqrt{2}+\left(\sqrt{2}+1\right)y-\sqrt{2}-1=0\)
\(\Leftrightarrow\left(-\sqrt{2}+1\right)x+\left(\sqrt{2}+1\right)y+1-2\sqrt{2}=0\)