trong mặt phẳng tọa độ Oxy, hình chiếu vuông góc của điểm A(2;1) lên đường thẳng d: 2x+y-7=0 có tọa độ là
K
Khách
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.
Những câu hỏi liên quan
CM
5 tháng 7 2019
Đáp án A
Hình chiếu vuông góc của điểm M(x;y;z) trên mặt phẳng (Oxy) là M'(x;y;0)
Cách giải: Hình chiếu vuông góc của A(3;2;-1) trên mặt phẳng (Oxy) là điểm H(3;2;0)
H
2 tháng 5 2023
Gọi \(AH\) là hình chiếu của \(A\) trên \(d\)
\(\Rightarrow AH:-2x+4y+c'=0\)
AH đi qua \(A\left(1;1\right)\Rightarrow-2.1+4.1+c'=0\)
\(\Rightarrow c'=-2\)
\(\Rightarrow\) phương trình \(AH\) là : \(-2x+4y-2=0\Rightarrow-x+2y-1=0\)
Tọa độ H là nghiệm của hệ phương trình :
\(\left\{{}\begin{matrix}-x+2y-1=0\\4x+2y+1=0\end{matrix}\right.\Rightarrow\left\{{}\begin{matrix}x=-\dfrac{2}{5}\\y=\dfrac{3}{10}\end{matrix}\right.\)
\(\Rightarrow H\left(-\dfrac{2}{5};\dfrac{3}{10}\right)\)
2 tháng 5 2023
Gọi \(\left(d'\right)\) là đường thẳng qua A và vuông góc với (d). Do (d) có VTPT \(\overrightarrow{n_d}=\left(4;2\right)\)
\(\Rightarrow\) \(\left(d'\right)\) có VTPT \(\overrightarrow{n_{d'}}=\left(2;-4\right)\) hay \(\left(d'\right):2x-4y+m=0\) \(\left(m\inℝ\right)\)
Mà \(A\left(1;1\right)\in\left(d'\right)\) nên \(2-4+m=0\Leftrightarrow m=2\). Vậy đường thẳng qua A và vuông góc với \(d\) có pt là \(2x-4y+2=0\) hay \(x-2y+1=0\)
Do đó hình chiếu vuông góc H của A lên d chính là giao điểm của d' và d. Nếu \(H\) có tọa độ \(\left(x_H;y_H\right)\) thì \(x_H;y_H\) thỏa mãn hệ phương trình \(\left\{{}\begin{matrix}x_H-2y_H+1=0\\4x_H+2y_H+1=0\end{matrix}\right.\) \(\Leftrightarrow\left\{{}\begin{matrix}x_H=-\dfrac{2}{5}\\y_H=\dfrac{3}{10}\end{matrix}\right.\)\(\Rightarrow H\left(-\dfrac{2}{5};\dfrac{3}{10}\right)\).
Vậy hình chiếu của A lên d có tọa độ \(\left(-\dfrac{2}{5};\dfrac{3}{10}\right)\)
CM
1 tháng 6 2018
Đáp án C
Hình chiếu vuông góc của M(2;-1;4) lên mặt phẳng (Oxy) là điểm H(2;-1;0).
CM
21 tháng 3 2017
Đáp án A.
Tọa độ điểm M 2 ; − 1 ; 1 trên mặt phẳng (Oxy) là M ' 2 ; − 1 ; 0 .
CM
30 tháng 8 2018
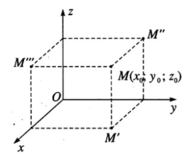
Gọi M’, M’’, M’’’ lần lượt là hình chiếu vuông góc của điểm M trên các mặt phẳng (Oxy), (Oyz), (Ozx).
Ta có:
• M’( x 0 ; y 0 ; 0)
• M’’ (0; y 0 ; z 0 )
• M’’’( x 0 ; 0; z 0 )
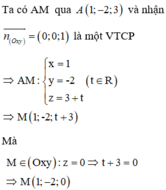
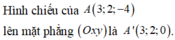
giả sử có một đường thẳng d' đi qua A và vuông góc với d. Do đường thẳng d có véc tơ pháp tuyến là \(\overrightarrow{n}\)= (2;1) nên suy ra véc tơ pháp tuyến của đường thẳng d' là \(\overrightarrow{n'}\)= (1;-2) mà đường thẳng d' đi qua điểm A(2;1) .Suy ra
phương trình của đường thẳng d' có dạng:
1(x-2) - 2(y-1) =0
⇔x - 2y =0
Suy ra tọa độ của hình chiếu H của A lên đường thẳng d là nghiệm của phương trình:
\(\left\{{}\begin{matrix}x-2y=0\\2x+y-7=0\end{matrix}\right.\) ⇔ \(\left\{{}\begin{matrix}x=\dfrac{14}{5}\\y=\dfrac{7}{5}\end{matrix}\right.\)
vậy .........