Trong không gian với hệ trục tọa độ Oxyz, cho điểm M (1;1;1). Mặt phẳng (P) đi qua M và cắt chiều dương của các trục Ox, Oy, Oz lần lượt tại các điểm A, B, C thỏa mãn OA = 2OB. Tính giá trị nhỏ nhất của thể tích khối tứ diện OABC.
K
Khách
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.
Những câu hỏi liên quan


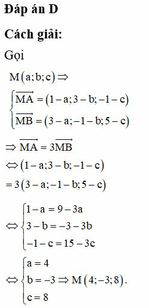



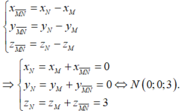


Chọn D
Giả sử A (a; 0; 0), B (0; b; 0), C (0; 0; c) với a, b, c > 0
Khi đó mặt phẳng (P) có dạng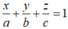 .
.
Vì (P) đi qua M nên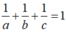
Mặt khác OA = 2OB nên a = 2b nên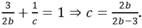
Thể tích khối tứ diện OABC là: V= abc/6
Ta có: