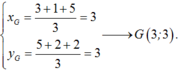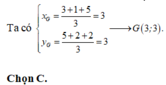Trong mật phẳng tọa độ Oxy , cho tam giác ABC có trọng tâm G(2;-3) và B(1;1) . Đương thẳng △ : x-y-4=0 đi qua A và đường phân giác trong góc A cắt BC tại điểm I sao cho diện tích tam giác IAB = \(\dfrac{4}{5}\) diện tích tam giác IAC . Biết điểm A có hoành độ dương . Viết phương trình tổng quát của đường thẳng BC
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

Tọa độ trọng tâm G x G ; y G là x G = 1 − 2 + 5 3 = 4 3 y G = 3 + 4 + 3 3 = 10 3 .
Chọn D.

Do C thuộc Ox nên tọa độ có dạng: \(C\left(x;0\right)\)
Do trọng tâm G thuộc Oy \(\Rightarrow x_G=0\)
Mà \(x_A+x_B+x_C=3x_G\)
\(\Rightarrow1+\left(-3\right)+x=3.0\)
\(\Rightarrow x=2\)
\(\Rightarrow C\left(2;0\right)\)

Gọi \(\left(x_G;y_G\right)\) là tọa độ của G. Theo công thức tính trọng tâm tam giác, ta có :
\(\begin{cases}x_G=\frac{-1+4+0}{3}=1\\y_G=\frac{0+0+m}{3}=\frac{m}{3}\end{cases}\)
Vậy \(G\left(1;\frac{m}{3}\right)\)
\(\widehat{AGB}=90^0\Leftrightarrow\overrightarrow{BG}\perp AG\Leftrightarrow\overrightarrow{BG}.\overrightarrow{AG}=0\) (1)
\(\overrightarrow{BG}=\left(1-4;\frac{m}{3}-0\right)=\left(-3;\frac{m}{3}\right)\)
\(\overrightarrow{AG}=\left(1+1;\frac{m}{3}-0\right)=\left(2;\frac{m}{3}\right)\)
\(\overrightarrow{BG}.\overrightarrow{AG}=\frac{m^2}{9}-6\) (2)
Thay (2) vào (1) ta có : \(\widehat{AGB}=90^0\Leftrightarrow m^2=54\Leftrightarrow m=\pm3\sqrt{6}\)
Vậy có 2 giá trị cần tìm của m