Cho △ A B C có A(0;2), B(4;0), C(1;1), và G là trọng tâm. Điểm M thuộc đường thẳng y=2 sao cho M A → + M B → + M C → nhỏ nhất, khi đó tọa độ M G → là
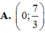
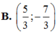
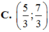
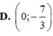
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.



Từ a+b+c=0 => b+c=-a
Theo đề ra ta có a3 + b3 + c3 = 0
=> a3 + (b+c)(b2 - bc + c2 )=0
<=> a3- a[(b + c )2 -3bc]= 0
<=> a3- [( -a )2 - 3bc] = 0
<=> a3 - a3 +3bc = 0
<=> 3bc= 0
<=> a =0 hoặc b=0 hoặc c=0 ( đpcm)
cho mik điểm nha bạn ơiii




Ta có: AB → = (−a; b; 0) và AC → = (−a; 0; c)
Vì AB → . AC → = a 2 > 0 nên góc ∠ BAC là góc nhọn.
Lập luận tương tự ta chứng minh được các góc ∠ B và ∠ C cũng là góc nhọn.

\(\left(x-a\right)\left(x-b\right)+\left(x-b\right)\left(x-c\right)+\left(x-c\right)\left(x-a\right)=0\\ \Leftrightarrow x^2-ax-bx+ab+x^2-bx-cx+bc+x^2-cx-ax+ac=0\\ \Leftrightarrow3x^2-2\left(a+b+c\right)x+ab+bc+ca=0\left(1\right)\)
pt(1) là pt bậc 2 ẩn x có:
\(\Delta'=\left(-a-b-c\right)^2-3\left(ab+bc+ca\right)\\ =a^2+b^2+c^2+2ab+2bc+2ca-3\left(ab+bc+ca\right)\\ =a^2+b^2+c^2-ab-bc-ca\\ =\dfrac{1}{2}\left[\left(a-b\right)^2+\left(b-c\right)^2+\left(c-a\right)^2\right]\)
pt có no kép nên delta' =0
nên: \(\dfrac{1}{2}\left[\left(a-b\right)^2+\left(b-c\right)^2+\left(c-a\right)^2\right]=0\\ \Rightarrow a-b=b-c=c-a=0\\ \Rightarrow a=b=c\)
bonus: khi đó pt: \(3\left(x-a\right)^2=0\Leftrightarrow x-a=0\Leftrightarrow x=a\)
=> x=a=b=c
ĐÁP ÁN: D