trong mặt phẳng Oxy cho hình chữ nhật ABCD có H là hình chiếu vuông góc của A trên BD. biết M (6;3), N (5;0) theo thứ tự là trung điểm của BH, CD .Điểm A thuộc đường thẳng d: 4x-y + 5 = 0. Xác định tọa độ các đỉnh A,B,C,D
K
Khách
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.
Những câu hỏi liên quan
CM
13 tháng 6 2017
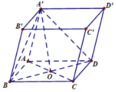
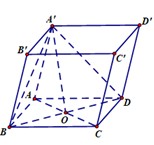
Đáp án C.
Kẻ A H ⊥ B D H ∈ B D mà
A ' O ⊥ A B C D ⇒ A ' O ⊥ A H ⇒ A H ⊥ A ' B D .
Ta có d B ' , A ' B D = d A , A ' B D = A H = A B . A D A B 2 + A D 2 = a 3 2
CM
25 tháng 4 2019
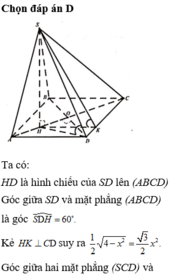
Chọn đáp án D
Ta có: HD là hình chiếu của SD lên mặt phẳng (ABCD).
Góc giữa SD và mặt phẳng (ABCD) là góc S D H ^ = 60 °
Kẻ HK
⊥
CD suy ra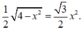 
Góc giữa hai mặt phẳng (SCD) và (ABCD) là góc S K H ^ = α
Ta có: 
Mặt khác: HK//AD 
Vậy: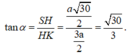 
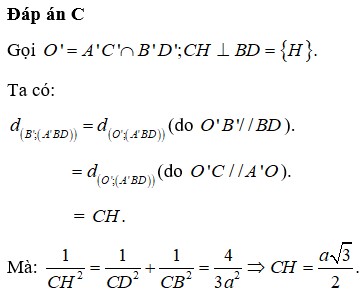
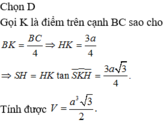
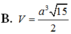
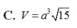
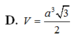
A B C D H M N P
Kẻ MP//AB \(\left(P\in AH\right)\) \(\Rightarrow MP\perp AD\)
\(\Rightarrow P\) là trực tâm tam giác \(ADM\Rightarrow DP\perp AM\)
Mặt khác theo cách dựng, MP là đường trung bình tam giác HAB
\(\Rightarrow MP=\frac{1}{2}AB=\frac{1}{2}CD=ND\)
\(\Rightarrow MNDP\) là hình bình hành (2 cạnh đối MP, DN song song và bằng nhau)
\(\Rightarrow DP\perp MN\Rightarrow MN\perp AM\)
Do \(A\in d\Rightarrow A\left(a;4a+5\right)\Rightarrow\left\{{}\begin{matrix}\overrightarrow{MA}=\left(a-6;4a+2\right)\\\overrightarrow{NM}=\left(1;3\right)\end{matrix}\right.\)
\(\overrightarrow{MA}.\overrightarrow{NM}=0\Leftrightarrow a-6+3\left(4a+2\right)=0\Rightarrow a=0\Rightarrow A\left(0;5\right)\)
Gọi \(B\left(b;c\right)\Rightarrow\left\{{}\begin{matrix}H\left(12-b;6-c\right)\\\overrightarrow{AB}=\left(b;c-5\right)\end{matrix}\right.\) và \(\overrightarrow{MB}=\left(b-6;c-3\right)\)
\(\overrightarrow{AB}=2\overrightarrow{DN}\Rightarrow D\left(\frac{10-b}{2};\frac{5-c}{2}\right)\Rightarrow\overrightarrow{DM}=\left(\frac{b+2}{2};\frac{c+1}{2}\right)\)
Do D, M, B thẳng hàng \(\Rightarrow\frac{b+2}{2\left(b-6\right)}=\frac{c+1}{2\left(c-3\right)}\Rightarrow b=2c\) \(\Rightarrow\left\{{}\begin{matrix}D\left(5-c;\frac{5-c}{2}\right)\\\overrightarrow{AB}=\left(2c;c-5\right)\\\overrightarrow{AD}=\left(5-c;\frac{-c-5}{2}\right)\end{matrix}\right.\)
\(\overrightarrow{AB}.\overrightarrow{AD}=0\Leftrightarrow2c\left(5-c\right)-\left(c-5\right)\left(\frac{c+5}{2}\right)=0\) \(\Rightarrow\left[{}\begin{matrix}c=5\\c=-1\end{matrix}\right.\)
\(\Rightarrow\left[{}\begin{matrix}B\left(10;5\right);D\left(0;0\right);C\left(10;0\right)\\B\left(-2;-1\right);D\left(6;3\right);C\left(4;-3\right)\end{matrix}\right.\)
//Dài quá, ko biết có cách ngắn hơn ko