Gọi d là đường thẳng đi qua A(2;0) có hệ số góc m cắt đồ thị tại ba điểm phân biệt A,B,C Gọi B',C' lần lượt là hình chiếu vuông góc của B,C lên trục tung. Tìm giá trị dương của m để hình thang BB'C'C có diện tích
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

a)Gọi pt đường thẳng d là: \(y=ax+b\left(a\ne0\right)\)
Vì d có hệ số góc là k \(\Rightarrow a=k\)
Vì (d) đi qua điểm \(A\left(-2;-1\right)\Rightarrow-1=-2k+b\Rightarrow b=\dfrac{1}{2k}\)
\(\Rightarrow\left(d\right):y=kx+\dfrac{1}{2k}\)
b) Vì điểm \(B\in\left(P\right)\Rightarrow y_B=-2x_B^2=-2\Rightarrow B\left(1;-2\right)\)
\(\Rightarrow-2=k+\dfrac{1}{2k}\Leftrightarrow-2=\dfrac{2k^2+1}{2k}\Rightarrow-4k=2k^2+1\)
\(\Rightarrow2k^2+4k+1=0\)
\(\Delta=4^2-4.2=8\)
\(\Rightarrow\left[{}\begin{matrix}k=\dfrac{-b-\sqrt{\Delta}}{2a}=\dfrac{-4-\sqrt{8}}{4}=\dfrac{-2-\sqrt{2}}{2}\\k=\dfrac{-b+\sqrt{\Delta}}{2a}=\dfrac{-4+\sqrt{8}}{4}=\dfrac{-2+\sqrt{2}}{2}\end{matrix}\right.\)

Chọn D
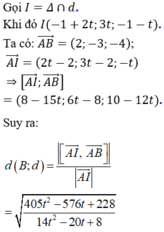
Xét hàm số:
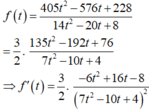
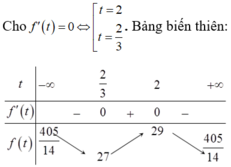
Do đó d (B; d) nhỏ nhất khi f(t) đạt giá trị nhỏ nhất bằng 27 tại t = 2/3. Suy ra ![]() . Chọn một vectơ chỉ phương của đường thẳng d là
. Chọn một vectơ chỉ phương của đường thẳng d là ![]()
Vậy phương trình đường thẳng ![]()
Đáp án là C.
Không mất tính tổng quát, giả sử
x C > x B .
Ta có: d có phương trình
y = m x − 2 .
Phương trình hoành độ giao điểm:
m x − 2 = − x 3 + 6 x 2 − 9 x + 2
⇔ x = 2 x 2 − 4 x + 1 + m = 0
Để tồn tại A, B, thì phương trình x 2 − 4 x + m + 1 = 0 phải có 2 nghiệm phân biệt khác 2
⇔ m < 3 ⇒ x A = 2 ; x B + x C = 4 ; x B x C = m + 1 ; y C − y B = m x C − x B .
Trường hợp 1: ⇒ x B x C = m + 1 > 0 ⇔ − 1 < m < 3 * .
Ta có .
S B B ' C ' C = B B ' + C C ' . B ' C ' 2 = x B + x C . m x C − x B 2 = 8 ⇔ 4 m 16 − 4 m + 1 2 = 8
.
Đối chiếu điều kiện (*) ta được m=2.
Trường hợp 2:
x C > 0 > x B ⇒ x B x C = m + 1 < 0 ⇔ m < − 1 < 0
(Loại vì m > 0 ).