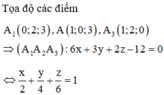Trong mặt phẳng với hệ trục tọa độ Oxy, cho A(2;-3), B(1;0) Phép tịnh tiến theo =(4;-3) biến điểm A, B tương ứng thành A’, B’. Khi đó, độ dài đoạn thẳng A’B’ bằng:
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

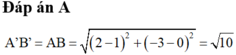

Giả sử tọa độ M(x;0). Khi đó \(\overrightarrow{MA}=\left(1-x;2\right);\overrightarrow{MB}=\left(4-x;3\right)\)
Theo giả thiết ta có \(\overrightarrow{MA}.\overrightarrow{MB}=MA.MB.\cos45^0\)
\(\Leftrightarrow\left(1-x\right)\left(4-x\right)+6=\sqrt{\left(1-x\right)^2+4}.\sqrt{\left(4-x\right)^2+9}.\frac{\sqrt{2}}{2}\)
\(\Leftrightarrow x^2-5x+10=\sqrt{x^2-2x+5}.\sqrt{x^2-8x+25}.\frac{\sqrt{2}}{2}\)
\(\Leftrightarrow2\left(x^2-5x+10\right)^2=\left(x^2-5x+10\right)\left(x^2-8x+25\right)\) (do \(x^2-5x+10>0\))
\(\Leftrightarrow x^4-10x^3+44x^2-110x+75=0\)
\(\Leftrightarrow\left(x-1\right)\left(x-5\right)\left(x^2-4x+15\right)=0\)
\(\Leftrightarrow x=1;x=5\)
Vậy ta có 2 điểm cần tìm là M(1;0) hoặc M(5;0)

![]()
![]()
Mặt phẳng cần tìm (P) đi qua M(0;0;2) và nhận k → = 0 , 0 , 1 làm một VTPT nên có phương trình (P): z - 2 = 0
Chọn A.

Đáp án C
Hình chiếu vuông góc của M(2;-1;4) lên mặt phẳng (Oxy) là điểm H(2;-1;0).

Trung điểm I của AB là: \(I\left(5;6\right)\)
Ta gọi pt đường thẳng AB có dạng: \(y=ax+b\)
\(\rightarrow\left\{{}\begin{matrix}5=a.4+b\\7=a.6+b\end{matrix}\right.\rightarrow\left\{{}\begin{matrix}a=1\\b=1\rightarrow\end{matrix}\right.AB:y=x+1\)
Gọi pt đường trung trực của AB là: \(y=ax+b\left(1\right)\)
Do (d) vuông góc với AB và d đi qua I nên:
\(\rightarrow\left\{{}\begin{matrix}a.1=-1\\6=a.4+b\end{matrix}\right.\)\(\rightarrow\left\{{}\begin{matrix}a=-1\\b=10\end{matrix}\right.\)\(\rightarrow\left(d\right):y=-x+10\)

Chọn C.
Phương pháp:
Viết phương trình đường thẳng dưới dạng phương trình đoạn chắn.
Cách giải:
![]()

gọi Pt đường thảng .....y=ax+b(d)
d đi qua M(-1,1) 1=-a+b⇔b=a+1
gọi d cắt Ox tại \(A\left(-\dfrac{b}{a},O\right)\)
d cắt Oy tại \(B\left(O,b\right)\)
\(\Delta AOB\) vuông cân tại o
\(\Rightarrow OA=OB\Rightarrow\left(-\dfrac{b}{a}\right)^2+o^2=o^2+b^2\)
\(\dfrac{b^2}{a^2}=b^2\Leftrightarrow\dfrac{1}{a^2}=1\Leftrightarrow a^2=1\)
\(\Leftrightarrow\left[{}\begin{matrix}a=1\\a=-1\end{matrix}\right.\Rightarrow\left[{}\begin{matrix}b=2\\b=0\left(loại\right)\end{matrix}\right.\)
(do d cắt 2 trục tọa độ nên a,b≠0)
vậy PtT đg thảng d:y=x+2
Gọi pt đường thẳng có dạng \(y=ax+b\)
Đường thẳng qua M tạo 2 trục tọa độ 1 tam giác vuông cân khi nó có hệ số góc \(a=1\) hoặc \(a=-1\)
\(\Rightarrow\left[{}\begin{matrix}y=x+b\\y=-x+b\end{matrix}\right.\)
Thay tọa độ M vào phương trình ta được:
\(\left[{}\begin{matrix}1=-1+b\\1=-\left(-1\right)+b\end{matrix}\right.\) \(\Rightarrow\left[{}\begin{matrix}b=2\\b=0\end{matrix}\right.\)
Có 2 đường thẳng thỏa mãn: \(\left[{}\begin{matrix}y=x+2\\y=-x\end{matrix}\right.\)