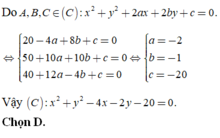Cho ∆ABC có B(2;-7), pt đường cao quá A là 3x+y+11=0, pt đường trung tuyến qua C là x+2y+7=0. Viết pt các cạnh của ∆ABC.
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.


1. \(2cosB=\sqrt{2}\Rightarrow cosxB=\dfrac{\sqrt{2}}{2}\Rightarrow B=45^0\)
2. \(A=180^0-\left(B+C\right)=60^0\)
3. \(r=\dfrac{S}{p}=\sqrt{3}\)
4. \(R=\dfrac{abc}{4S}=\dfrac{65}{8}\)

\(\Rightarrow\left\{{}\begin{matrix}\overrightarrow{AB}=\left(2,2\right)\\\overrightarrow{BC}=\left(-5,-1\right)\\\overrightarrow{AC}=\left(-3,1\right)\end{matrix}\right.\Rightarrow\left\{{}\begin{matrix}AB=\sqrt{2^2+2^2}=2\sqrt{2}\\BC=\sqrt{\left(-5\right)^2+\left(-1\right)^1}=\sqrt{26}\\AC=\sqrt{\left(-3\right)^2+1^2}=\sqrt{10}\end{matrix}\right.\)
\(p=\dfrac{2\sqrt{2}+\sqrt{26}+\sqrt{10}}{2}\)
Áp dụng công thức Herong:
\(S=\sqrt{p.\left(p-2\sqrt{2}\right)\left(p-\sqrt{26}\right)\left(p-\sqrt{10}\right)}=\sqrt{16}=4\)

Đáp án C
Ta có: ![]()
Từ điểm D kẻ đường thẳng song song với AC, cắt cạnh AB tại điểm E. Từ D kẻ đường thẳng song song với AB cắt cạnh AC tại F. Do AD là đường phân giác trong của tam giác ABC nên ta suy ra AEDF là hình thoi.
Đặt AE=AF=k. Ta có:
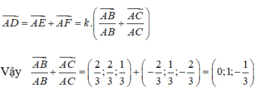
là một vectơ chỉ phương của đường thẳng AD. Từ đó suy ra C là khẳng định đúng.
Ta cũng lưu ý rằng khẳng định A sai, do tam giác ABC không cân tại đỉnh A.

a: Xét ΔABC có
\(cosB=\dfrac{BA^2+BC^2-AC^2}{2\cdot BA\cdot BC}\)
=>\(\dfrac{4+12-AC^2}{2\cdot2\cdot2\sqrt{3}}=cos30=\dfrac{\sqrt{3}}{2}\)
=>\(16-AC^2=4\cdot2\sqrt{3}\cdot\dfrac{\sqrt{3}}{2}=12\)
\(\Leftrightarrow AC^2=4\)
=>AC=2
Xét ΔABC có AB=AC
nên ΔABC cân tại A
=>\(\widehat{BAC}=\dfrac{180^0-\widehat{B}}{2}=120^0\)
ΔABC cân tại A
=>\(\widehat{ABC}=\widehat{ACB}=30^0\)
b: Kẻ CH vuông góc AB
=>CH=hC
\(\widehat{CAH}+\widehat{CAB}=180^0\)(hai góc kề bù)
=>\(\widehat{CAH}+120^0=180^0\)
=>\(\widehat{CAH}=60^0\)
Xét ΔCAH vuông tại H có \(sinCAH=\dfrac{CH}{CA}\)
=>\(\dfrac{CH}{1}=sin60=\dfrac{\sqrt{3}}{2}\)
=>\(CH=\dfrac{\sqrt{3}}{2}\)
Gọi M là trung điểm của AC
=>BM=mb
M là trung điểm của AC
=>AM=AC/2=1
Xét ΔAMB có \(cosMAB=\dfrac{AM^2+AB^2-MB^2}{2\cdot MA\cdot AB}\)
=>\(\dfrac{1^2+2^2-MB^2}{2\cdot1\cdot2}=cos120=\dfrac{-1}{2}\)
=>\(5-MB^2=-2\)
=>\(MB^2=7\)
=>\(MB=\sqrt{7}\)