Trong mặt phẳng Oxy, cho các điểm A(-3;3), B(1;4), C(2;-5). Tọa độ điểm M thõa mãn \(2\vec{MA} \)\(-\vec{BC} \)\(=4\vec{CM} \)
mn giải giúp tui nha năn nỉ mn đó
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

a)
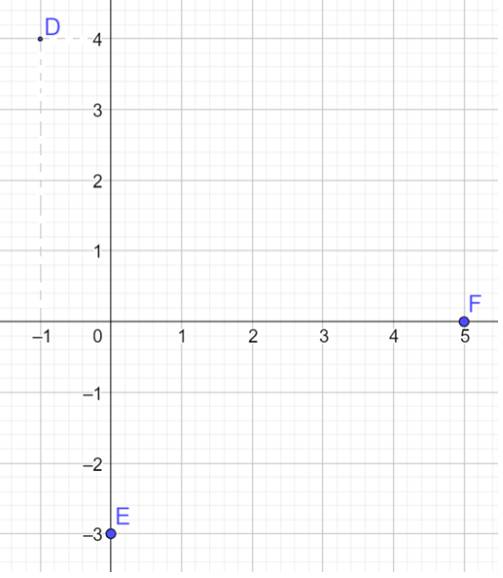
b) Vì tọa độ vectơ \(\overrightarrow {OM} \) chính là tọa độ của điểm M (với mọi M) nên ta có:
\(\overrightarrow {OD} = \left( { - 1;4} \right),\overrightarrow {OE} = \left( {0; - 3} \right),\overrightarrow {OF} = \left( {5;0} \right)\)
c)
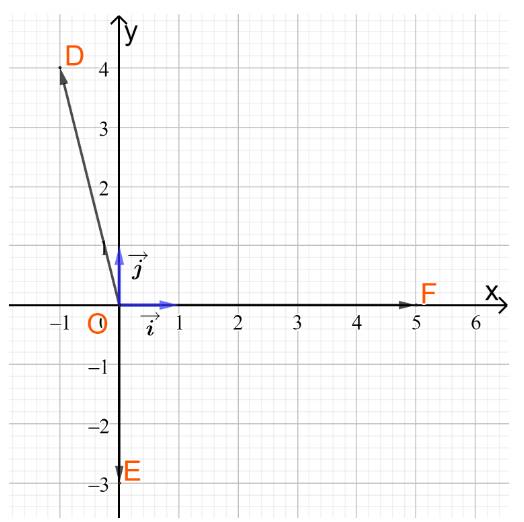
Từ hình vẽ ta có tọa độ của hai vectơ và \(\overrightarrow j \)là
và \(\overrightarrow j = (0;1)\)

\(a,\) Thay \(x=3;y=4\Rightarrow\dfrac{4}{3}\cdot3=4\) (đúng)
Vậy \(A\left(3;4\right)\in y=\dfrac{4}{3}x\)
Dù hiểu đề là tìm tọa độ điểm $M$ nhưng lần sau bạn vẫn cần viết đầy đủ yêu cầu của đề ra nhé.
Lời giải:
Giả sử tọa độ điểm $M$ là $(a,b)$
\(\overrightarrow{MA}=(-3-a; 3-b)\)
\(\overrightarrow{BC}=(1;-9)\)
\(\overrightarrow{CM}=(a-2; b+5)\)
Để $2\overrightarrow{MA}-\overrightarrow{BC}=4\overrightarrow{CM}$ thì:
\(\Leftrightarrow 2(-3-a; 3-b)-(1;-9)=4(a-2; b+5)\)
\(\Leftrightarrow \left\{\begin{matrix} 2(-3-a)-1=4(a-2)\\ 2(3-b)+9=4(b+5)\end{matrix}\right.\Leftrightarrow \left\{\begin{matrix} a=\frac{1}{6}\\ b=\frac{-5}{6}\end{matrix}\right.\)
Vâng e cám mơn