Giá trị thực của m để hàm số y = x - m 2 x + 1 đạt GTLN bằng 3 trên [-4;-2] là
A. m = ± 1
B. m = ± 5
C. m = 5
D. m = 1
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

Ta có đạo hàm y’ = 3( x+ m) 2≥0 với mọi x.
=> Hàm số đồng biến trên đoạn [1; 2] nên hàm số đạt GTLN tại x = 2.
Khi đó; y( 2) = 8 khi và chỉ khi : ( 2+m) 3 = 8 hay m= 0
Chọn C.

Đáp án B.
Phương pháp:
Sử dụng cách vẽ đồ thị hàm số y = f x
Cách giải:
Xét hàm số y = x 2 + 2 x + m − 4 = f x có:
y ' = 2 x + 2
y ' = 0 ⇔ x = − 1
Bảng biến thiên:
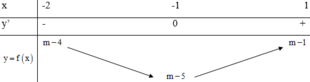
+) m ≥ 5 :
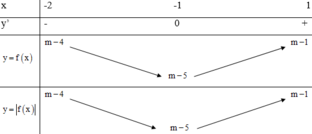
M a x − 2 ; 1 x 2 + 2 x + m − 4 = f 1 = m − 1 = 4 ⇒ m = 5
(Thỏa mãn)
+) 4 ≤ m < 5 :
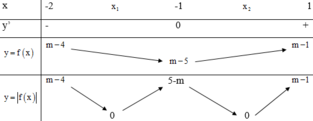
M a x − 2 ; 1 x 2 + 2 x + m − 4 = M a x m − 1 ; 5 − m = 4
Mà
m − 1 > 5 − m , ∀ m ∈ 4 ; 5 ⇒ m − 1 = 4 ⇒ m = 5
(loại)
+) 1 ≤ m < 4 :
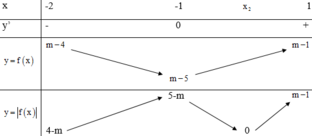
M a x − 2 ; 1 x 2 + 2 x + m − 4 = M a x 5 − m ; m − 1 = 4.
m ∈ − 1 ; 3 ⇒ max y = 5 − m = 4 ⇔ m = 1 t m
m ∈ − 1 ; 3 ⇒ max y = m − 1 = 4 ⇔ m = 5 k t m
+) m < 1 :

M a x − 2 ; 1 x 2 + 2 x + m − 4 = 5 − m = 4 ⇒ m = 1
(Không thỏa mãn)
Vậy m ∈ 4 ; 1 , có hai giá trị của m thỏa mãn.
Chọn A
Tập xác định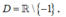
Ta có: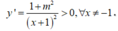 Suy ra hàm số y =
x
-
m
2
x
+
1
đồng biến trên
Suy ra hàm số y =
x
-
m
2
x
+
1
đồng biến trên 
Do đó:
Theo giả thiết: