Question

[Julian Edward]

Trong hệ tọa độ, cho tam giác \(A\left(3;1\right)\), B(-1;5) và C(3;-2)

a) Lập pt đg thg d có hệ số góc \(k=\frac{5}{3}\)

b) Tính chiều cao từ C của tam giác ABC

c) với điểm M thuộc đường thẳng \(d:2x-y-3=0\) sao cho MA=MB. Tính diện tích tam giác ABM

Answer 1

[Nguyễn Việt Lâm]

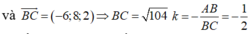
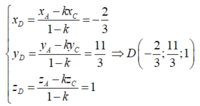
Gọi phương trình d có dạng \(y=\frac{5}{3}x+b\)

Do d qua A nên: \(\frac{5}{3}.3+b=1\Rightarrow b=-4\)

Vậy pt d là: \(y=\frac{5}{3}x-4\Leftrightarrow5x-3y-12=0\)

Answer 2

[Nguyễn Việt Lâm]

a/ Đề thiếu, đường thẳng d qua đâu nữa bạn?

b/ \(\overrightarrow{BA}=\left(4;-4\right)=4\left(1;-1\right)\) \(\Rightarrow\) pt AB có dạng:

\(1\left(x-3\right)+1\left(y-1\right)=0\Leftrightarrow x+y-4=0\)

\(\Rightarrow\) Chiều cao từ C của tam giác ABC bằng khoảng cách từ C đến AB

\(d\left(C;AB\right)=\frac{\left|3-2-4\right|}{\sqrt{1^2+1^2}}=\frac{3\sqrt{2}}{2}\)

c/ Do M thuộc d \(\Rightarrow M\left(m;2m-3\right)\Rightarrow\left\{{}\begin{matrix}\overrightarrow{AM}=\left(m-3;2m-4\right)\\\overrightarrow{BM}=\left(m+1;2m-8\right)\end{matrix}\right.\)

\(MA=BM\Leftrightarrow\left(m-3\right)^2+\left(2m-4\right)^2=\left(m+1\right)^2+\left(2m-8\right)^2\)

\(\Leftrightarrow12m-48=0\Rightarrow m=4\Rightarrow M\left(4;5\right)\)

\(AB=\sqrt{4^2+\left(-4\right)^2}=4\sqrt{2}\) ; \(d\left(M;AB\right)=\frac{\left|4+5-4\right|}{\sqrt{1^2+1^2}}=\frac{5\sqrt{2}}{2}\)

\(\Rightarrow S_{ABM}=\frac{1}{2}.d\left(M;AB\right).AB=10\)