Trong không gian Oxyz, phương trình mặt phẳng (P) đi qua hai điểm A(1;-7;-8), B(2;-5;-9) sao cho khoảng cách từ điểm M(7;-1;-2) đến (P) lớn nhất có một vecto pháp tuyến là . Giá trị của tổng a + b là
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

Đáp án C
Ta có n P → 1 ; 0 ; 0 ; n Q → 0 ; 1 ; − 1 suy ra n → = n P → ; n Q → = 0 ; 1 ; 1
Suy ra phương trình mặt phẳng cần tìm là: y + z − 5 = 0

Đáp án D
Ta có: A B → = ( - 3 ; - 2 ; 2 ) ; n ( P ) → = ( 1 ; - 3 ; 2 )
Khi đó: A B → ; n ( P ) → = 0 ; 8 ; 12 ⇒ n ( Q ) → = ( 0 ; 2 ; 3 )
Suy ra (Q): 2y + 3z – 11 = 0

Đáp án D
Gọi d = P ∩ Q ,d có VTCP là u → .
Khi đó u → = 1 ; − 1 ; 0 , 2 ; 0 ; 4 = − 4 ; − 4 ; 2 = − 2 2 ; 2 ; − 1 .
Mặt phẳng (R) qua A 1 ; 2 ; 3 , có VTCP là 2 ; 2 ; − 1 và đi qua điểm B ( − 1 2 ; − 1 2 ; 0 ) thuộc giao tuyến, (R) có phương trình là R : x − y + 1 = 0.

Đáp án C
Phương trình mặt phẳng (Q) viết lại dưới dạng: 3x - 6y + 2z - 6 = 0
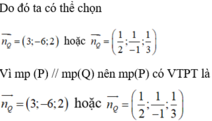
Suy ra đáp án B sai. Trong ba đáp án còn lại chỉ có mặt phẳng ở đáp án C đi qua điểm A.

Đáp án B
Vì (P) vuông góc với hai mặt phẳng (Oxy), (Oyz) và (Oxy) (Oyz) = Oy nên ta có (P) → Oy => n p → = j → = (0; 1; 0)
Từ đó suy ra phương trình của mặt phẳng (P) là: 0(x - 2) + 1(y - 6 ) + 0(z + 3) = 0 ⇔ y - 6 = 0

Đáp án A
Từ giả thiết suy ra:
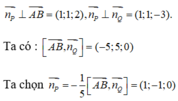
Từ đó suy ra phương trình của mặt phẳng (P) là:
1(x - 1) - 1(y - 0) + 0(z - 1) = 0 ⇔ x - y - 1 = 0


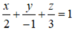
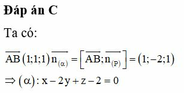
Đáp án D
Mặt phẳng cần tìm sẽ vuông góc với (ABM). Một vecto pháp tuyến của nó là tích có hướng của vecto pháp tuyến mặt phẳng (ABM) và A B →
Cũng có thể làm như sau: Khoảng cách lớn nhất là MH với H là hình chiếu vuông góc của M lên đường thẳng AB. Ta tìm được H(3;-3;-10)
d