Cho hàm số y=ax+b. Tìm a, b của hàm số này biết đồ thị (D) của hàm số này đi qua điểm A(2;-1) và cắt trục hoành tại điểm B có hoành độ là XB=\(\dfrac{3}{2}\). Tính khoảng cách từ gốc tọa độ O đến đường thẳng (D).
K
Khách
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.
Những câu hỏi liên quan
6 tháng 8 2023
b: Vì (d1)//(d) nên (d1): y=-2x+b
=>a=-2
Thay x=2 và y=1 vào (d1), ta được:
b-4=1
=>b=5
a: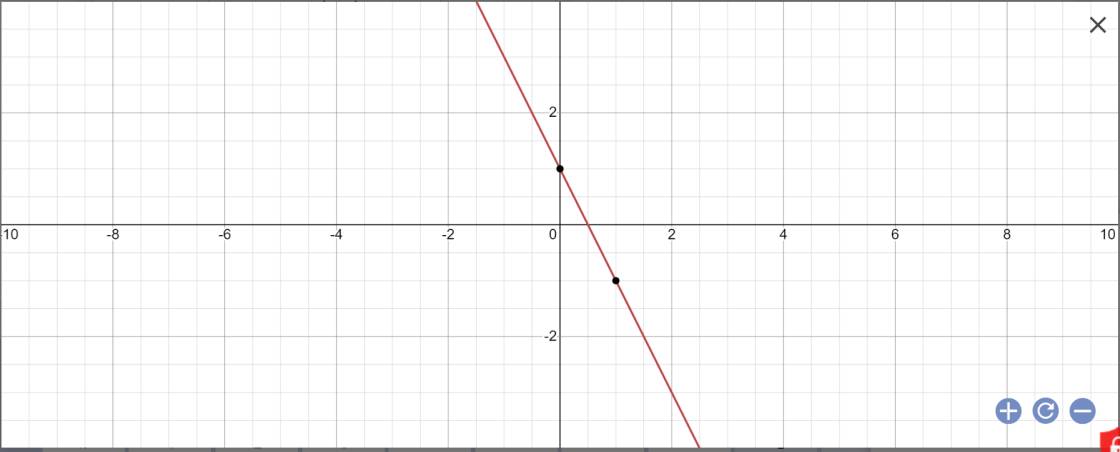 
1 tháng 12 2021
\(a,\Leftrightarrow a+3=4\Leftrightarrow a=1\\ \Leftrightarrow y=x+3\\ c,\text{PT hoành độ giao điểm: }x+3=2x+5\Leftrightarrow x=-2\Leftrightarrow y=1\Leftrightarrow A\left(-2;1\right)\\ \text{Vậy tọa độ giao điểm 2 đths là }A\left(-2;1\right)\)
22 tháng 12 2021
a: Thay x=-2 và y=3 vào (d), ta được:
-2a=3
hay a=-3/2
22 tháng 1 2022
a: Thay x=1 và y=-2 vào y=ax, ta được:
1xa=-2
hay a=-2
29 tháng 12 2021
b: Vì (d')//(d) nên a=2
Vậy: (d'): y=2x+b
Thay x=1 và y=4 vào (d'), ta được:
b+2=4
hay b=2
27 tháng 11 2023
a: Thay x=-2 và y=6 vào (d), ta được:
-2a+4=6
=>-2a=2
=>a=2/-2=-1
b: a=-1 nên \(y=-x+4\)
16 tháng 12 2021
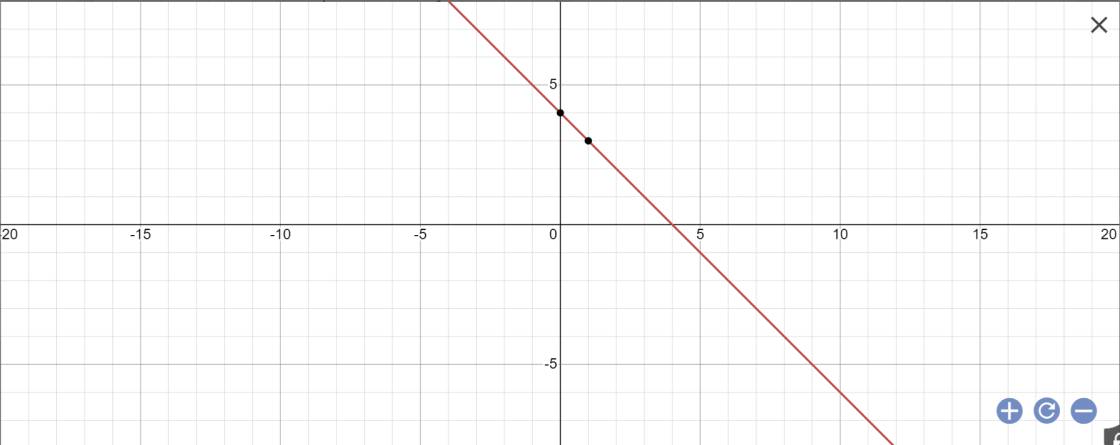
\(b,\) PT giao Ox và Oy:
\(y=0\Leftrightarrow x=2\Leftrightarrow A\left(2;0\right)\Leftrightarrow OA=2\\ x=0\Leftrightarrow y=-4\Leftrightarrow B\left(0;-4\right)\Leftrightarrow OB=4\)
Gọi H là chân đường cao từ O đến (d)
Áp dụng HTL: \(\dfrac{1}{OH^2}=\dfrac{1}{OA^2}+\dfrac{1}{OB^2}=\dfrac{1}{4}+\dfrac{1}{16}=\dfrac{5}{16}\)
\(\Leftrightarrow OH^2=\dfrac{16}{5}\Leftrightarrow OH=\dfrac{4}{\sqrt{5}}\left(cm\right)\)
Vậy k/c là \(\dfrac{4}{\sqrt{5}}\left(cm\right)\)
\(c,\Leftrightarrow\left\{{}\begin{matrix}a=2;b\ne-4\\0a+b=3\end{matrix}\right.\Leftrightarrow\left\{{}\begin{matrix}a=2\\b=3\end{matrix}\right.\)
25 tháng 12 2016
Sorry, mk chưa học đồ thị bn ơi, đừng giận nha Huyền Anh Kute 
25 tháng 12 2016
bn ns gì trong hộp tin nhắn vậy, mk ko thấy vì bị quảng cáo che mất rồi Huyền Anh Kute
Hoành độ là mấy vậy bạn?