Tìm các số phức z thỏa mãn và
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

z + 2 + i - z 1 + i = 0
z = - 2 + z + - 1 + z i
z = t > 0 ⇒ t = t - 2 2 + t - 1 2
⇔ t 2 - 6 t + 5 = 0 ⇔ t = 1 ; t = 5
Ta có t = 5 ( do t > 1 ) nên có
z = - 2 + z + - 1 + z i
= -2 + 5 + ( -1 + 5 )i = 3 + 4i
Đáp án cần chọn là D

Đáp án D.
Đặt
z = a + b i ⇒ a + b i + 2 + i − a 2 + b 2 1 + i = 0
⇔ a + 2 − a 2 + b 2 = 0 b + 1 − a 2 + b 2 = 0 ⇔ a + 2 = b + 1 b + 1 = a 2 + b 2 ⇔ a = b − 1 b ≥ − 1 b 2 + 2 b + 1 = a 2 + b 2 ⇔ a = b − 1 b ≥ − 1 2 b + 1 = b − 1 2 ⇔ b = 0 ; a = − 1 b = 4 ; a = 3 .
Do z > 1 ⇒ a = 3 , b = 4.

Đáp án D
z + 2 + i − z ( 1 + i ) = 0 ⇔ ( a + b i ) + 2 + i − a 2 + b 2 ( 1 + i ) = 0 ⇔ a + 2 − a 2 + b 2 + ( b + 1 − a 2 + b 2 ) i = 0 ⇒ a + 2 − a 2 + b 2 = 0 b + 1 − a 2 + b 2 = 0 ⇒ a − b + 1 = 0 ⇒ a = b − 1 ⇒ b + 1 − ( b − 1 ) 2 + b 2 = 0 ⇒ 2 b 2 − 2 b + 1 = b + 1 ⇒ b ≥ − 1 b 2 − 4 b = 0 ⇒ b = 0 b = 4 ⇒ a = − 1 ( L ) a = 3 ⇒ P = 4 + 3 = 7
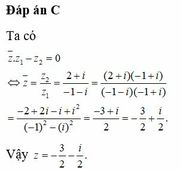
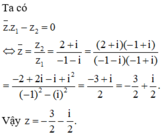


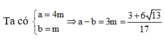

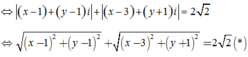


Chọn D.