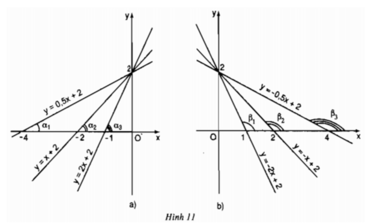
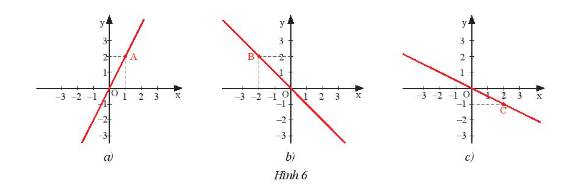
Hình 22a, biểu diễn đồ thị của các hàm số bậc nhất: y = 0,5x + 2; y = 2x + 2. Hình 22b biểu diễn đồ thị của các hàm số bậc nhất: y = -2x + 2; y = -0,5x + 2
a) Quan sát hình 22a, so sánh các góc α,βvà so sánh các giá trị tương ứng của hệ số của x trong các hàm số bậc nhất rồi rút ra nhận xét.
b) Quan sát hình 22b, so sánh các góc α′,β′và so sánh các giá trị tương ứng của hệ số của x trong các hàm số bậc nhất rồi rút ra nhận xét.
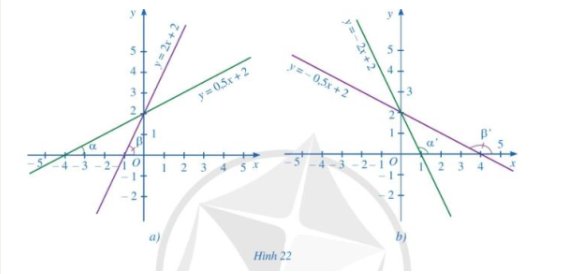

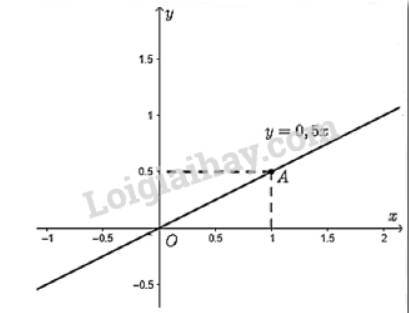



a) Quan sát hình 22a ta thấy: \(\widehat \alpha < \widehat \beta \)
- Hệ số x của hàm số y = 0,5x + 2 là 0,5
- Hệ số x của hàm số y = 2x + 2 là 2
Nhận xét:
- Khi hệ số của x > 0 => góc tạo bởi đường thẳng đó với trục Ox là góc nhọn.
- Hệ số của x càng nhỏ => góc tạo bởi đường thẳng đó với trục Ox càng nhỏ.
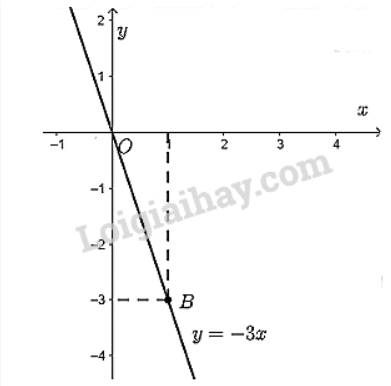
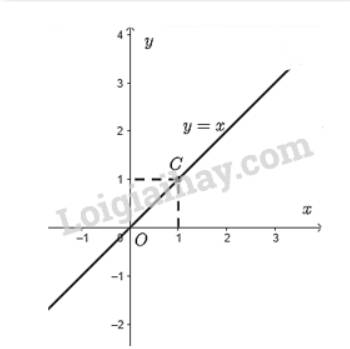
b) Quan sât hình 22b ta thấy: \(\widehat {\alpha '} < \widehat {\beta '}\)
- Hệ số x của hàm số y = -0,5 x + 2 là -0,5
- Hệ số x của hàm số y = -2x + 2 là -2
Ta thấy: - 0,5 > -2
Nhận xét:
- Khi hệ số của x < 0 => góc tạo bởi đường thẳng đó với trục Ox là góc tù.
- Hệ số của x càng nhỏ => góc tạo bởi đường thẳng đó với trục Ox càng nhỏ.