Kiểm tra xem:
b) Mỗi số x = 1; x = 3 có phải là một nghiệm của đa thức Q(x) = x2 – 4x + 3 không.
K
Khách
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.
Những câu hỏi liên quan
17 tháng 10 2019
Gọi số điểm 4 bài đầu là a, điểm bài cuối là b
\(\Rightarrow\hept{\begin{cases}a,b\inℕ\\a,b\le100\\\frac{4a+b}{5}=82\end{cases}\Leftrightarrow4a+b=410}\)
Lại có \(\hept{\begin{cases}a\le100\Rightarrow b\ge10\\410\equiv2\left(mod4\right),4a⋮4\end{cases}\Rightarrow\hept{\begin{cases}10\le b\le100\\b\equiv2\left(mod4\right)\end{cases}}}\)
\(\Rightarrow b\in\left\{10;14;18;...;94;98\right\}\)
Số điểm kiểm tra cuối của Laila có thể nhận số giá trị là:
\(\left(98-10\right):4+1=23\left(gt\right)\)
vậy ...
17 tháng 10 2019
Có 5 đáp án cho sẵn của bài là:
(A)4 (B)5 (C)9 (D)10 (E)18
Đè thi thử AMC 8 2018
NV
Nguyễn Việt Lâm
Giáo viên
24 tháng 12 2022
Chọn ngày kiểm tra môn toán: 6 cách, chọn ngày kiểm tra môn văn: 5 cách, chọn ngày kiểm tra môn anh: 4 cách
\(\Rightarrow\) Không gian mẫu: \(6.5.4=120\) cách
Nếu toán kiểm tra vào thứ 4 => 2 môn còn lại chỉ có 3 ngày thứ 5, thứ 6, thứ 7 để kiểm tra nên ko thể xếp sao cho 2 môn này cách nhau ít nhất 1 ngày (loại)
\(\Rightarrow\) Toán chỉ có thể kiểm tra vào thứ 2 hoặc 3
TH1: toán kiểm tra vào thứ Hai: 2 môn còn lại có 3 cách xếp là 46,47,57. Hoán vị 2 môn này có 2 cách \(\Rightarrow2.3=6\)
TH2: toán kiểm tra vào thứ Ba: 2 môn còn lại chỉ có 1 cách là 57, hoán vị 2 môn này có 2 cách
Tổng cộng: \(6+2=8\) cách
Xác suất: \(P=\dfrac{8}{120}\)
E
1
4 tháng 3 2022
Ta có \(P\left(1\right)=1-4+3=0\)
Vậy x = 1 là nghiệm của đa thức trên
\(P\left(3\right)=9-12+3=0\)
Vậy x = 3 là nghiệm của đa thức trên
CM
1 tháng 12 2019
Ta có: Q(1) = 12 – 4.1 + 3 = 1 – 4 + 3 = 0
⇒ x = 1 là nghiệm của Q(x)
Q(3) = 32 – 4.3 + 3 = 9 – 12 + 3 = 0
⇒ x = 3 là nghiệm của Q(x)
Vậy x = 1 ; x = 3 là nghiệm của Q(x).
HQ
Hà Quang Minh
Giáo viên
17 tháng 9 2023
a) Thay các giá trị – 1, 0, 1, 2 vào biểu thức ta được:
\(\begin{array}{l}3.( - 1) - 6 = - 3 - 6 = - 9\\3.0 - 6 = 0 - 6 = - 6\\3.1 - 6 = 3 - 6 = - 3\\3.2 - 6 = 6 - 6 = 0\end{array}\)
Vậy 2 là nghiệm của đa thức \(3x - 6\).
b) Thay các giá trị – 1, 0, 1, 2 vào biểu thức ta được:
\(\begin{array}{l}{( - 1)^4} - 1 = 1 - 1 = 0\\{0^4} - 1 = 0 - 1 = - 1\\{1^4} - 1 = 1 - 1 = 0\\{2^4} - 1 = 16 - 1 = 15\end{array}\)
Vậy 1 và – 1 là nghiệm của đa thức \({x^4} - 1\)
c) Thay các giá trị – 1, 0, 1, 2 vào biểu thức ta được:
\(\begin{array}{l}3.{( - 1)^2} - 4.( - 1) = 3 + 4 = 7\\{3.0^2} - 4.0 = 0 - 0 = 0\\{3.1^2} - 4.1 = 3 - 4 = - 1\\{3.2^2} - 4.2 = 12 - 8 = 4\end{array}\)
Vậy 0 là nghiệm của đa thức \(3{x^2} - 4x\).
d) Thay các giá trị – 1, 0, 1, 2 vào biểu thức ta được:
\(\begin{array}{l}{( - 1)^2} + 9 = 1 + 9 = 10\\{0^2} + 9 = 0 + 9 = 9\\{1^2} + 9 = 1 + 9 = 10\\{2^2} + 9 = 4 + 9 = 13\end{array}\)
Vậy không giá trị nào là nghiệm của đa thức \({x^2} + 9\).
28 tháng 7 2023
b: Tham khảo:
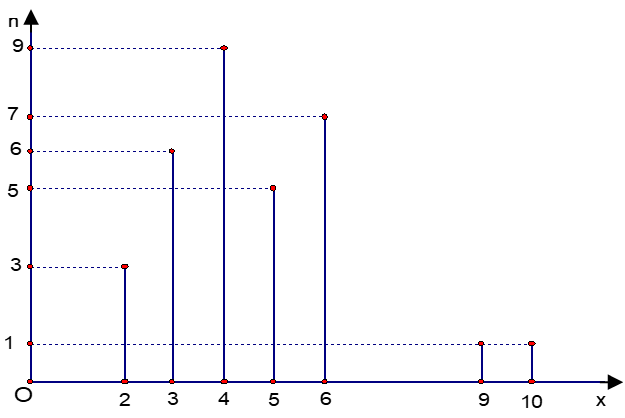
a: Số lỗi trung bình là;
\(\dfrac{2\cdot3+3\cdot6+4\cdot9+5\cdot5+6\cdot7+9\cdot1+10\cdot1}{3+6+9+5+7+1+1}\simeq4,6\)
b) Ta có: Q(1) = 12 – 4.1 + 3 = 1 – 4 + 3 = 0
=> x = 1 là nghiệm của Q(x)
Q(3) = 32 – 4.3 + 3 = 9 – 12 + 3 = 0
=> x = 3 là nghiệm của Q(x)