Vòng chạy quanh sân trường dài 400m. Hai hs chạy thi xuất phát từ 1 điểm. Biết vận tốc của các em lần lượt là v\(_1\) = 4,8m/s ; v2 = 4m/s . Tính thời gian ngắn nhất để hai em gặp nhau trên đường chạy
K
Khách
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.
Những câu hỏi liên quan
10 tháng 9 2018
Bài này không khó mà.
Vì 2 học sinh chạy xuất phát từ 1 điểm (đi cùng chiều) nên thời gian ngắn nhất để 2 em gặp nhau trên đường chạy là:
\(t=\frac{S}{v_1-v_2}=\frac{400}{4,8-4}=\frac{400}{0,8}=500\left(s\right)\)
Chúc bạn học tốt.
KC
26 tháng 2 2020
Giải:
Thời gian 2 bạn gặp nhau khi cả 2 chạy cùng chiều là:
\(t_1=\frac{s}{v_1-v_2}=\frac{400}{4,8-4}=500\left(s\right)\)
Thời gian 2 bạn gặp nhau khi cả 2 chạy ngược chiều là:
\(t_2=\frac{s}{v_1+v_2}=\frac{400}{4,8+4}=\frac{500}{11}\left(s\right)\)
Mặt khác: t2<t1 => thời gian ngắn nhất để 2 bạn gặp nhau trên đường chạy là sau \(\frac{500}{11}\left(s\right)\)kể từ lúc 2 bạn xuất phát từ 1 điểm
VT
12 tháng 2 2017
Em thứ nhất chạy nhanh hơn em thứ hai nên trong thời gian t0 = 1s em thứ nhất chạy hơn em thứ hai một đoạn đường là:
s = s1 – s2 = v1.t0 – v2.t0 = 4,8.1 – 4.1 = 0,8m.
Sau khoảng thời gian t (s), quãng đường em thứ nhất chạy hơn em thứ hai là:
S = 0,8.t
Em thứ nhất sẽ gặp em thứ hai lần đầu tiên sau thời gian t (s) khi mà quảng đường em thứ nhất chạy hơn em thứ hai trong khoảng thời gian đó bằng đúng chu vi một vòng chạy.
Khi đó ta có: S = 0,8.t = Cchu vi = 400 m
Suy ra (v1 – v2).t = 400.
Vậy thời gian ngắn nhất để hai em gặp nhau trên đường chạy là:
30 tháng 9 2016
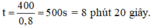
ptcđ của e hs 1 là:
S1 = 4,8.t
S2 = 4t
vì đây là sân hình tròn
=> chu kỳ S là 400m
2 gặp nhau khi
=> S1 = S2 + 400.k
lần gặp nhau lần gần nhất là k=1
=> S1= S2 +400
=> 4,8.t = 4t + 400
=> t= 500(s)
vậy sau 500s từ khi xuất phát 2 em sẽ gặp nhau
30 tháng 9 2016
Dương Thị Trà My là phương trình chuyển động nha pn
bài này thầy mk cho lm nhìu lần rùi nên chắc chắn nhé^^
DH
18 tháng 9 2019
Tham khảo:
Em thứ nhất chạy nhanh hơn em thứ hai nên trong thời gian t0 = 1s em thứ nhất chạy hơn em thứ hai một đoạn đường là:
s = s1 – s2 = v1.t0 – v2.t0 = 4,8.1 – 4.1 = 0,8m.
Em thứ nhất sẽ gặp em thứ hai lần đầu tiên sau thời gian t (s) khi mà quãng đường em thứ nhất chạy hơn em thứ hai trong t (s) bằng đúng chu vi một vòng chạy.
Khi đó ta có: v1.t – v2.t = Cchu vi = 400 m.
Suy ra (v1 – v2).t = 400.
Vậy thời gian ngắn nhất để hai em gặp nhau trên đường chạy là:
18 tháng 9 2019
Vì em thứ nhất chạy nhanh hơn em thứ hai nên trong một giây em thứ nhất vượt xa em thứ hai một đoạn đường là v1 – v2 = 0,8m.
Em thứ nhất muốn gặp em thứ hai trong khoảng thời gian ngắn nhất thì em thứ nhất phải vượt em thứ hai đúng 1 vòng sân.
Vậy thời gian ngắn nhất đê hai em gặp nhau trên đường chạy:
\(t=\frac{400}{0,8}=500s=80ph20s\)
HQ
Hà Quang Minh
Giáo viên
2 tháng 10 2023
Đổi 360 giây = 6 phút, 420 giây = 7 phút
Giả sử họ lại gặp nhau sau x (phút)( x > 0)
Vận động viên thứ nhất chạy một vòng sân hết 6 phút nên x là bội của 6.
Vận động viên thứ hai chạy một vòng sân hết 7 phút nên x là bội của 7.
Nên x ∈ BC(6, 7).
Mà x ít nhất nên x = BCNN(6, 7).
Ta có: 6 = 2.3; 7 = 7
x = BCNN(6, 7) = 2.3.7 = 42
Vậy sau 42 phút họ lại gặp nhau.
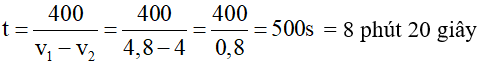
Vì 2 bạn chuyển động cùng chiều nên vận tốc của bạn 1 so với bạn 2 là :
v12 = v1 - v2 = 4,8 - 4 = 0,8 m/s
Khi 2 bạn gặp nhau tại 1 điểm trên đường chạy thì bạn thứ nhất chạy nhiều hơn bạn 2 một vòng sân
Thời gian 2 bạn gặp nhau là :
t = s/t = 400/0,8 = 500 (s) = 8 phút 20s.
Phương trình chuyển động của học sinh thứ nhất :
S1 = 4,8m/s
S2 = 4m/s
Mà đây là vòng tròn
=> Chu kì S là 400m
Hai em học sinh gặp nhau lúc :
S1 = S2 + 400
=> 4,8m/s = 4m/s + 400
=> Thời gian là 500 giây ( s )
Vậy sau 500 giây hai em gặp nhau trên đường chạy