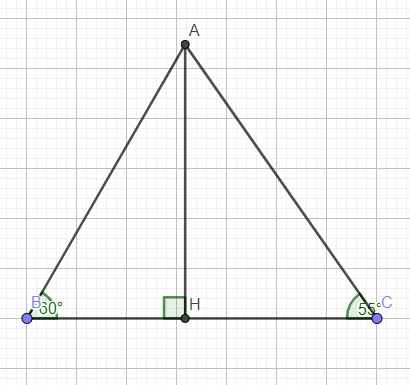
Cho tam giác ABC có \(\widehat{B}=\widehat{C}\)

GN

giúp nha

22 tháng 12 2021

Cho tam giác ABC có \(\widehat{B}=\widehat{C}\); tia phân giác của góc A cắt BC tại M. Trên tia đối của tia MA lấy điểm D sao MD = MA. a) Chứng minh: \(\Delta ABM=\Delta ACM\) b) Chứng minh: BC vuông góc với AM. c) Chứng minh: AB // CD .d) Cho biết, nếu\(\widehat{ACB}=55^o\), tính số...

Đọc tiếp

#Toán lớp 7

1

NL

Nguyễn Lê Phước Thịnh

22 tháng 12 2021

a: Xét ΔABM và ΔACM có

AB=AC

\(\widehat{BAM}=\widehat{CAM}\)

AM chung

Do đó: ΔABM=ΔACM

Đúng(1)

TT

Trần Thị Vân Ngọc

15 tháng 10 2017 - olm

a, Cho tam giác ABC biết \(\widehat{A}=100^o,\widehat{B}-\widehat{C}=50^o.Tính\widehat{B},\widehat{C}\)

b, Tam giác ABC có\(\widehat{B}=80^o,3\widehat{A}=2\widehat{C}.Tính\widehat{A},\widehat{C}\)

#Toán lớp 7

1

Q

QuocDat

15 tháng 10 2017

a)

=> Ta có : \(\widehat{A}+\widehat{B}+\widehat{C}\) = 180^o

100^o + \(\widehat{B}+\widehat{C}\) = 180^o

\(\widehat{B}+\widehat{C}\) = 180^o - 100^o

\(\widehat{B}+\widehat{C}\) = 80^o

Góc B = (80^o+50^o):2 = 65^o

=> \(\widehat{C}\) = 65^o - 50^o = 15^o

Vậy \(\widehat{B}\) = 65^o ; \(\widehat{C}\) = 15^o

b)

Ta có : \(\widehat{3A}+\widehat{B}+\widehat{2C}\) = 180^o

\(\widehat{3A}+\widehat{2C}\) = 180^o - 80^o

\(\widehat{3A}+\widehat{2C}\) = 100^o

=> \(\widehat{A}\) = 100^o:(3+2).3 = 60^o

\(\widehat{C}\) = 100^o - 60^o = 40^o

Vậy \(\widehat{A}\) = 60^o ; \(\widehat{C}\) = 40^o

Đúng(0)

DN

Duy Nguyễn Hoàn

12 tháng 1 2022

cho \(\Delta ABC\) có \(\widehat A={40^0}\) biết \(\widehat B= 3\widehat C\) tam giác abc là tam giác gì

giúp mik với

#Toán lớp 7

1

NL

Nguyễn Lê Phước Thịnh

12 tháng 1 2022

\(\widehat{B}+\widehat{C}=140^0\)

\(\Leftrightarrow4\cdot\widehat{C}=140^0\)

\(\Leftrightarrow\widehat{C}=35^0\)

hay \(\widehat{B}=105^0\)

Vậy: ΔABC tù

Đúng(0)

TP

Trường Phan

16 tháng 12 2021

Câu 25. Cho △ABC có \(\widehat{A}\) = 600 ; \(\widehat{B}\) = 3\(\widehat{C}\) là tam giác:A.Tam giác vuông B. Tam giác nhọnC. Tam giác tù D. Tam giác...

Đọc tiếp

#Toán lớp 7

5

I

ILoveMath

16 tháng 12 2021

A

Đúng(3)

LL

Liễu Lê thị

16 tháng 12 2021

B

Đúng(0)

QT

Quoc Tran Anh Le

Giáo viên

17 tháng 9 2023

Cho hai tam giác ABC và A’B’C’ thỏa mãn: BC = B’C’ = 3 cm, \(\widehat B = \widehat {B'} = 60^\circ ,\widehat C = 50^\circ ,\widehat {A'} = 70^\circ \). Hai tam giác ABC và A’B’C’ có bằng nhau không? Vì sao?

#Toán lớp 7

1

KS

Kiều Sơn Tùng

17 tháng 9 2023

Tổng ba góc trong một tam giác bằng 180°. Vậy trong tam giác A’B’C’ có \(\widehat {C'} = 180^\circ - 70^\circ - 60^\circ = 50^\circ \).

Xét hai tam giác ABC và A’B’C’ có:

\(\widehat B = \widehat {B'} = 60^\circ ;\)

BC = B’C’ ( = 3 cm)

\(\widehat C = \widehat {C'} = 50^\circ \)

Vậy \(\Delta ABC = \Delta A'B'C'\)(g.c.g)

Đúng(0)

QT

Quoc Tran Anh Le

Giáo viên

24 tháng 9 2023

Cho tam giác ABC có AB = 12; \(\widehat B = {60^o}\); \(\widehat C = {45^o}\). Tính diện tích của tam giác ABC.

#Toán lớp 10

1

HQ

Hà Quang Minh

Giáo viên

24 tháng 9 2023

Áp dụng định lí sin trong tam giác ABC, ta có:

\(\frac{{AC}}{{\sin B}} = \frac{{AB}}{{\sin C}}\)

\( \Rightarrow AC = \sin B.\frac{{AB}}{{\sin C}} = \sin {60^o}.\frac{{12}}{{\sin {{45}^o}}} = 6\sqrt 6 \)

Lại có: \(\widehat A = {180^o} - ({60^o} + {45^o}) = {75^o}\)

\( \Rightarrow \)Diện tích tam giác ABC là:

\(S = \frac{1}{2}AB.AC.\sin A = \frac{1}{2}.12.6\sqrt 6 .\sin {75^o} \approx 85,2\)

Vậy diện tích tam giác ABC là 85,2.

Đúng(0)

NK

Nguyễn Khánh Phương

27 tháng 7 2021

Bài 1: Cho tam giác ABC có \(\widehat{B}=60^o\), \(\widehat{C}=55^o\), AC = 4,5cm. Tính diện tích tam giác ABC?

#Toán lớp 9

2

NV

Nguyễn Việt Lâm

Giáo viên

27 tháng 7 2021

Kẻ đường cao AH ứng với BC

Trong tam giác vuông ACH:

\(sinC=\dfrac{AH}{AC}\Rightarrow AH=AC.sinC\)

\(cosC=\dfrac{CH}{AC}\Rightarrow CH=AC.cosC\)

Trong tam giác vuông ABH:

\(tanB=\dfrac{AH}{BH}\Rightarrow BH=\dfrac{AH}{tanB}=\dfrac{AC.sinC}{tanB}\)

Do đó:

\(S_{ABC}=\dfrac{1}{2}AH.BC=\dfrac{1}{2}AH\left(BH+CH\right)=\dfrac{1}{2}.4,5.sin55^0.\left(\dfrac{4,5.sin55^0}{tan60^0}+4,5.cos55^0\right)\approx8,68\left(cm^2\right)\)

Đúng(2)

NV

Nguyễn Việt Lâm

Giáo viên

27 tháng 7 2021

undefined

Đúng(0)

DV

Duy Vũ

17 tháng 1 2023 - olm

Cho tam giác ABC có \(\widehat{A}=2\widehat{B}\) , \(\widehat{C}\) tù và các cạnh đều là số nguyên dương. Tìm giá trị nhỏ nhất của chu vi tam giác ABC.

#Toán lớp 10

0

QT

Quoc Tran Anh Le

Giáo viên

25 tháng 9 2023

Cho tam giác ABC có \(a = 8,b = 10,c = 13.\) Tính các góc \(\widehat A,\widehat B,\widehat C.\)

a) Tam giác ABC có góc tù không?

b) Tính độ dài trung tuyến AM, diện tích tam giác và bán kính đường tròn ngoại tiếp tam giác đó.

c) Lấy điểm D đối xứng với A qua C.

#Toán lớp 10

1

KS

Kiều Sơn Tùng

25 tháng 9 2023

Tham khảo:

a) Áp dụng hệ quả của định lí cosin, ta có:

\(\begin{array}{l}\cos A = \frac{{{b^2} + {c^2} - {a^2}}}{{2bc}};\cos B = \frac{{{a^2} + {c^2} - {b^2}}}{{2ac}}\\ \Rightarrow \left\{ \begin{array}{l}\cos A = \frac{{{{10}^2} + {{13}^2} - {8^2}}}{{2.10.13}} = \frac{{41}}{{52}} > 0;\\\cos B = \frac{{{8^2} + {{13}^2} - {{10}^2}}}{{2.8.13}} = \frac{{133}}{{208}} > 0\\\cos C = \frac{{{8^2} + {{10}^2} - {{13}^2}}}{{2.8.10}} = - \frac{1}{{32}} < 0\end{array} \right.\end{array}\)

\( \Rightarrow \widehat C \approx 91,{79^ \circ } > {90^ \circ }\), tam giác ABC có góc C tù.

b)

+) Áp dụng định lí cosin trong tam giác ACM, ta có:

\(\begin{array}{l}A{M^2} = A{C^2} + C{M^2} - 2.AC.CM.\cos C\\ \Leftrightarrow A{M^2} = {8^2} + {5^2} - 2.8.5.\left( { - \frac{1}{{32}}} \right) = 91,5\\ \Rightarrow AM \approx 9,57\end{array}\)

+) Ta có: \(p = \frac{{8 + 10 + 13}}{2} = 15,5\).

Áp dụng công thức heron, ta có: \(S = \sqrt {p(p - a)(p - b)(p - c)} = \sqrt {15,5.(15,5 - 8).(15,5 - 10).(15,5 - 13)} \approx 40\)

+) Áp dụng định lí sin, ta có:

\(\frac{c}{{\sin C}} = 2R \Rightarrow R = \frac{c}{{2\sin C}} = \frac{{13}}{{2.\sin 91,{{79}^ \circ }}} \approx 6,5\)

c)

Ta có: \(\widehat {BCD} = {180^ \circ } - 91,{79^ \circ } = 88,{21^ \circ }\); \(CD = AC = 8\)

Áp dụng định lí cosin trong tam giác BCD, ta có:

\(\begin{array}{l}B{D^2} = C{D^2} + C{B^2} - 2.CD.CB.\cos \widehat {BCD}\\ \Leftrightarrow B{D^2} = {8^2} + {10^2} - 2.8.10.\cos 88,{21^ \circ } \approx 159\\ \Rightarrow BD \approx 12,6\end{array}\)

Đúng(0)

RC

Rùa Con Chậm Chạp

1 tháng 2 2019 - olm

1. Cho tam giác ABC có \(\widehat{C}< \widehat{B}< 90^o\). Vẽ đường phân giác AD và đường cao AH của tam giác ABC. CMR: \(\widehat{DAH}=\frac{1}{2}\left(\widehat{ABC}-\widehat{ACB}\right)\)

#Toán lớp 7

0

QT

Quoc Tran Anh Le

Giáo viên

17 tháng 9 2023

Cho hai tam giác ABC và A’B’C’ thỏa mãn: AB = A’B’, \(\widehat A = \widehat {A'},\widehat C = \widehat {C'}\). Hai tam giác ABC và A’B’C’ có bằng nhau không? Vì sao?

#Toán lớp 7

1

KS

Kiều Sơn Tùng

17 tháng 9 2023

Vì \(\widehat A = \widehat {A'},\widehat C = \widehat {C'}\)mà tổng ba góc trong một tam giác bằng 180° nên \(\widehat B = \widehat {B'}\).

Xét hai tam giác ABC và A’B’C’ có: \(\widehat A = \widehat {A'}\), AB = A’B’, \(\widehat B = \widehat {B'}\).

Vậy \(\Delta ABC = \Delta A'B'C'\)(g.c.g)

Đúng(0)

Chúng tôi đề xuất

Tài nguyên

Ứng dụng mobile

Bảng xếp hạng

Các khóa học có thể bạn quan tâm

Yêu cầu VIP