Một con lắc lò xo nằm ngang dao động theo phương trình (x tính bằng cm; t tính bằng s). Kể từ t = 0, lò xo không biến dạng lần đầu tại thời điểm
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

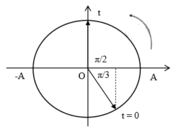
Lò xo không biến dạng tại vị trí cân bằng.
→ Biểu diễn dao động của vật tương ứng trên đường tròn.
Từ hình vẽ ta thấy rằng khoảng thời gian tương ứng là t = 5T/12 = 5/12
Đáp án A

Đáp án D
Phương pháp: Sử dụng lí thuyết về lực đàn hồi trong dao động điều hòa của CLLX ngang và đường tròn lượng giác
Cách giải:
+ Đối với CLLX ngang thì lực đàn hồi đổi chiều tại VTCB
+ Biểu diễn trên đường tròn lượng giác :
Góc quét được:
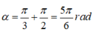
=> Từ t = 0 thì vật đi qua VTCB lần đầu tại thời điểm:
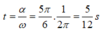

\(l_{max}=l_0+\Delta l+A\Rightarrow\left\{{}\begin{matrix}A=5cm=0,02m\\\Delta l=\dfrac{g}{\omega^2}=\dfrac{10}{\left(10\right)^2}=0,1m\\l_0=0,2m\end{matrix}\right.\)
=> \(l_{max}=0,2+0,1+0,02=0,32\left(m\right)=32cm\)
\(l_{min}=l_0+\Delta l-A=0,2+0,1-0,02=0,28\left(m\right)=28\left(cm\right)\)
Vậy ...

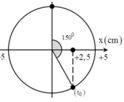
+ Lò xo không biến dạng tại vị trí cân bằng.
→ Biểu diễn dao động của vật tương ứng trên đường tròn.
+ Từ hình vẽ ta thấy rằng khoảng thời gian tương ứng là t = 5 12 T = 5 12 s
Đáp án A

Chọn C
+ ω = 2π : T = 20 rad/s.
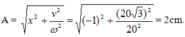
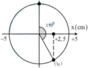
+ t = 0: x = 2cosφ = -1 => 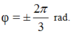
v = -40 sinφ > 0 => sinφ < 0 => ![]()
Vậy: x = 2 cos(20t - 2π/3) = 2 sin(20t - π/6) cm.
Chọn đáp án A
Lò xo không biến dạng tại vị trí cân bằng.
→ Biểu diễn dao động của vật tương ứng trên đường tròn.
Từ hình vẽ ta thấy rằng khoảng thời gian tương ứng là