Cho a ∈ Z ; b ∈ N* ; n ∈ N*. Chứng minh rằng:
a) Nếu a < b thì \(\dfrac{a}{b}< \dfrac{a+n}{b+n}\)
b) Nếu a > b thì \(\dfrac{a}{b}>\dfrac{a+n}{b+n}\)
c) Nếu a = b thì \(\dfrac{a}{b}=\dfrac{a+n}{b+n}\)
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

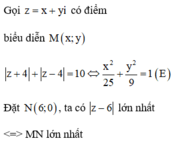
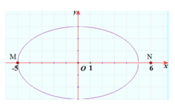
Vẽ trên hệ trục Oxy, nhận thấy MN lớn nhất khi M. Khi đó ![]()
Chọn B

Đáp án D.
Đặt z = a + bi => a + bi ![]()
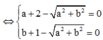
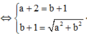
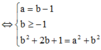

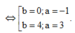
Do |z| > 1 => a = 3, b = 4
a)
\(a< b\Leftrightarrow a.n< b.n\) ( Vì \(a\in Z;b\in\) N*\(;n\in\) N* )
\(\Leftrightarrow ab+a.n< ab+b.n\)
\(\Leftrightarrow a\left(b+n\right)< b\left(a+n\right)\)
\(\Leftrightarrow\dfrac{a}{b}< \dfrac{a+n}{b+n}\) ( đpcm )
Vậy........
b)
\(a>b\Leftrightarrow a.n>b.n\)
\(\Leftrightarrow ab+a.n>ab+b.n\)
\(\Leftrightarrow a\left(b+n\right)>b\left(a+n\right)\)
\(\Leftrightarrow\dfrac{a}{b}>\dfrac{a+n}{b+n}\) ( đpcm )
Vậy.........
c)
\(a=b\Leftrightarrow a.n=b.n\)
\(\Leftrightarrow ab+a.n=ab+b.n\)
\(\Leftrightarrow a\left(b+n\right)=b\left(a+n\right)\)
\(\Leftrightarrow\dfrac{a}{b}=\dfrac{a+n}{b+n}\) ( đpcm )
Vậy............
Thanks ạ <3 <3