Con lắc lò có có k=40N/m ; m=100g. a) Tính chu kì, tần số, tần số góc b) Kéo vật ra khỏi vị trí cân bằng 5cm rồi thả nhẹ (bỏ qua ma sát). Tính năng lượng của vật, v của vật khi bằng nhau, độ lớn giá tốc cực đại.
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.


Đáp án C
Tại vị trí cân bằng, lò xo đã dãn một đoạn ∆ l 0 . Vật nặng chịu tác dụng của hai lực cân bằng, trọng lực và lực đàn hồi. Vậy:


Tại vị trí cân bằng, lò xo đã dãn một đoạn ∆ l 0 . Vật nặng chịu tác dụng của hai lực cân bằng, trọng lực và lực đàn hồi. Vậy:
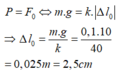
Lực đàn hồi cực đại tác dụng lên vật là:
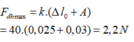
Đáp án C

Chọn đáp án B
+ Con lắc dao động cưỡng bức với tần số góc là ω = 10 rad / s và biên độ A = 10cm
→ a max = A . ω 2 = 100 cm / s 2

 Đáp án A
Đáp án A
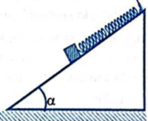
Chọn Ox như hình vẽ
Xét ở vị trí cân bằng các lực tác dụng vào vật bằng O:


A=\(\frac{l_{max}-l_{min}}{2}=\frac{20-14}{2}=3\).F=kA=40.0,03=1,2(N)

Đáp án A
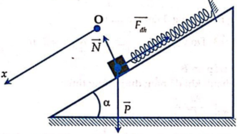
+ Do bỏ qua ma sát nên cơ năng của con lắc lò xo bảo toàn.
+ Khi ∆ l m a x = 4cm = 0,04m thì thế năng lớn nhất động năng bằng O.
+ Khi vmax thì động năng lớn nhất thế năng bằng O.
+ Theo bảo toàn cơ năng ta có:
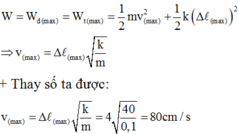

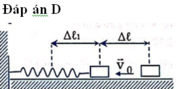
- Áp dụng định luật bảo toàn năng lượng cho quá trình chuyển động từ vị trí lò xo dãn cực đại ![]() đến vị trí lò xo nén cực đại
đến vị trí lò xo nén cực đại ![]() (từ phải qua trái) là
(từ phải qua trái) là
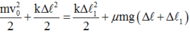
Với ![]() : là độ nén cực đại của lò xo.
: là độ nén cực đại của lò xo.
![]() : là độ dãn cực đại của lò xo.
: là độ dãn cực đại của lò xo.
- Áp dụng định luật bảo toàn năng lượng cho quá trình chuyển động ngược lại (từ trái qua phải) là
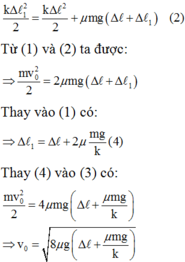
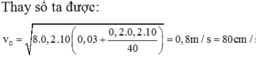

Đáp án A
+ Do bỏ qua ma sát nên cơ năng của con lắc lò xo bảo toàn.
+ Khi ∆ l m a x = 4cm = 0,04m thì thế năng lớn nhất động năng bằng O.
+ Khi vmax thì động năng lớn nhất thế năng bằng O.
+ Theo bảo toàn cơ nằng ta có:
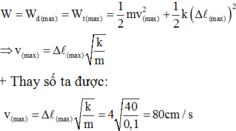
a) Chu kì: \(T=2\pi\sqrt{\dfrac{m}{k}}=2\pi\cdot\sqrt{\dfrac{0,1}{40}}=\dfrac{\pi}{10}s\)
Tần số: \(f=\dfrac{1}{2\pi}\sqrt{\dfrac{k}{m}}=\dfrac{1}{2\pi}\sqrt{\dfrac{40}{0,1}}=\dfrac{10}{\pi}\left(Hz\right)\)
Tần số góc: \(\omega=\sqrt{\dfrac{k}{m}}=\sqrt{\dfrac{40}{0,1}}=20\left(rad/s\right)\)
b) Năng lượng của vật: \(W=\dfrac{kA^2}{2}=\dfrac{40\cdot5^2}{2}=500\left(J\right)\)
Ta có: \(\Delta l=\dfrac{mg}{k}=\dfrac{0,1\cdot10}{40}=\dfrac{1}{40}\left(m\right)=2,5\left(cm\right)\)
\(\Rightarrow t=2\cdot\dfrac{\alpha}{\omega}=2\cdot\dfrac{arccos\dfrac{2,5}{5}}{20}=2\cdot\dfrac{\dfrac{\pi}{3}}{20}=\dfrac{\pi}{30}\left(s\right)\)
Vận tốc:
\(\Rightarrow v=\dfrac{s}{t}=\dfrac{5}{\dfrac{\pi}{30}}=\dfrac{1,5}{\pi}\left(m/s\right)\)
Gia tốc cực đại:
\(a_{max}=A\omega^2=5\cdot20^2=2000m/s^2\)