Mạch xoay chiều RLC mắc nối tiếp với \(R = 10\Omega \), cảm kháng \(Z_L = 10\Omega \); dung kháng \(Z_C = 5\Omega \) ứng với tần số \(f\). Khi \(f\) thay đổi đến giá trị \(f’\) thì trong mạch có cộng hưởng điện. Ta có
A.\(f’ = f.\)
B.\(f’ = 4f.\)
C.\(f’ < f. \)
D.\(f’= 2f.\)

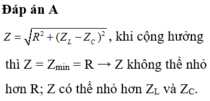

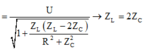
\(Z_L>Z_C\)
Để xảy ra cộng hưởng điện thì giảm \(Z_L\) và tăng \(Z_C\)
-> Tần số phải giảm
-> f' < f
ZL=2.Zc => L.w= \(\frac{2}{w.C}\) => f=\(\frac{2}{2\eta.\sqrt{LC}}\)
f' có CHD => f' = \(\frac{1}{2\eta\sqrt{LC}}\) => f' < f => C.