Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.
Giao điểm A của d1 và d2 là nghiệm:
\(\left\{{}\begin{matrix}x+2y+1=0\\x+y-5=0\end{matrix}\right.\) \(\Rightarrow\left\{{}\begin{matrix}x=11\\y=-6\end{matrix}\right.\)
\(\Delta\) song song d3 nên nhận (2;3) là 1 vtpt, nên có pt:
\(2\left(x-11\right)+3\left(y+6\right)=0\Leftrightarrow2x+3y-4=0\)
a: Phương trình hoành độ giao điểm là:
2x+1=x+1
=>2x-x=1-1
=>x=0
Thay x=0 vào y=x+1, ta được:
y=0+1=1
=>A(0;1)
b: Vì (d4) có hệ số góc là -4 nên (d4): y=-4x+b
Thay x=0 và y=1 vào (d4), ta được:
b-4*0=1
=>b=1
=>y=-4x+1
c: Vì (d5)//(d6) nên (d5): y=0,5x+a
Thay x=0 và y=1 vào (d5), ta được:
a+0,5*0=1
=>a=1
=>y=0,5x+1
d: Thay x=0 và y=1 vào (d3), ta được:
0*(m+1)+2m-1=1
=>2m-1=1
=>2m=2
=>m=1
Lời giải:
VTPT của $(d)$: $(2,-3)$
Đường thẳng $\Delta$ vuông góc với $(d)$ nên VTCP của $(\Delta)$ chính là $(2,-3)$
$\Rightarrow$ VTPT $ của $(\Delta)$ là $(3,2)$
PTĐT $(\Delta)$: $3(x-1)+2(y-2)=0$
$\Leftrightarrow 3x+2y-7=0$
Denta tạo với d1, d2 1 tam giác cân với đỉnh là giao điểm của d1, d2 khi và chỉ khi denta vuông góc phân giác tạo bởi d1, d2
Gọi \(A\left(x;y\right)\) là 1 điểm bất kì thuộc phân giác tạo bởi 2 đường thẳng d1, d2
\(\Rightarrow\dfrac{\left|x-7y+17\right|}{\sqrt{1^2+\left(-7\right)^2}}=\dfrac{\left|x+y-5\right|}{\sqrt{1^2+1^2}}\Leftrightarrow\left|x-7y+17\right|=\left|5x+5y-25\right|\)
\(\Leftrightarrow\left[{}\begin{matrix}5x+5y-25=x-7y+17\\5x+5y-25=-x+7y-17\end{matrix}\right.\)
\(\Leftrightarrow\left[{}\begin{matrix}x+3y+\dfrac{21}{2}=0\\3x-y-4=0\end{matrix}\right.\)
\(\Rightarrow\Delta\) nhận \(\left(3;-1\right)\) hoặc \(\left(1;3\right)\) là 1 vtpt
Có 2 đường thẳng thỏa mãn:
\(\left[{}\begin{matrix}3\left(x-0\right)-1\left(y-1\right)=0\\1\left(x-0\right)+3\left(y-1\right)=0\end{matrix}\right.\)
Đáp án D
+Giao điểm của d1 và d2 là nghiệm của hệ
+Lấy M(1 ; 0) thuộc d1. Tìm M’ đối xứng M qua d2
+Viết phương trình đường thẳng ∆ đi qua M và vuông góc với d2 là
3(x-1) + 1( y=0) =0 hay 3x+ y-3= 0
Gọi H là giao điểm của ∆ và đường thẳng d2. Tọa độ H là nghiệm của hệ
Ta có H là trung điểm của MM’. Từ đó suy ra tọa độ:
Viết phương trình đường thẳng d đi qua 2 điểm A và M’ : đi qua A(0 ;1) , vectơ chỉ phương 
=> vectơ pháp tuyến 
Gọi M là giao điểm \(d_1;d_2\Rightarrow\) tọa độ M thỏa mãn:
\(\left\{{}\begin{matrix}x+2y-1=0\\x-3y+3=0\end{matrix}\right.\) \(\Rightarrow\left\{{}\begin{matrix}x=-\dfrac{3}{5}\\y=\dfrac{4}{5}\end{matrix}\right.\) \(\Rightarrow M\left(-\dfrac{3}{5};\dfrac{4}{5}\right)\)
Chọn \(N\left(1;0\right)\) là 1 điểm thuộc \(d_1\)
Gọi \(d_3\) là đường thẳng qua N và vuông góc \(d_2\Rightarrow d_3\) nhận (3;1) là 1 vtpt
Phương trình \(d_3\):
\(3\left(x-1\right)+1\left(y-0\right)=0\Leftrightarrow3x+y-3=0\)
Gọi P là giao điểm \(d_2;d_3\Rightarrow\) tọa độ P là nghiệm:
\(\left\{{}\begin{matrix}3x+y-3=0\\x-3y+3=0\\\end{matrix}\right.\) \(\Rightarrow P\left(\dfrac{3}{5};\dfrac{6}{5}\right)\)
Gọi Q là điểm đối xứng N qua \(d_2\Rightarrow P\) là trung điểm NQ
\(\Rightarrow\left\{{}\begin{matrix}x_Q=2x_P-x_N=\dfrac{1}{5}\\y_Q=2y_P-y_N=\dfrac{12}{5}\end{matrix}\right.\) \(\Rightarrow Q\left(\dfrac{1}{5};\dfrac{12}{5}\right)\)
\(\Rightarrow MQ\) đối xứng \(MN\) qua \(d_2\Rightarrow MQ\) là đường thẳng d cần tìm
\(\overrightarrow{MQ}=\left(\dfrac{4}{5};\dfrac{8}{5}\right)=\dfrac{4}{5}\left(1;2\right)\) \(\Rightarrow\) đường thẳng d nhận (2;-1) là 1 vtpt
Phương trình d:
\(2\left(x-\dfrac{1}{5}\right)-1\left(y-\dfrac{12}{5}\right)=0\Leftrightarrow2x-y+2=0\)
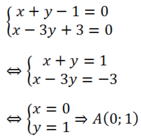
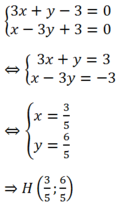
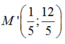
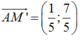
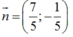
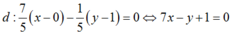
a) Giao điểm d1 và d2
\(\left\{{}\begin{matrix}x+3y-1=0\\x-3y-5=0\end{matrix}\right.\) \(\Leftrightarrow\left\{{}\begin{matrix}x=-2\\y=1\end{matrix}\right.\) => A (-2;1)
Đường thẳng d3 có \(\overrightarrow{n_{d3}}=\left(2;-1\right)\) . Delta vuông góc với d3 nên có
\(\overrightarrow{u_{\Delta}}=\left(2;-1\right)\) \(\Rightarrow\overrightarrow{n_{\Delta}}=\left(-1;-2\right)\)
PTđt delta
\(-1\left(x+2\right)+\left(-2\right)\left(y-1\right)=0\)
\(\Leftrightarrow-x-2y+1=0\)
b) Tương tự, tìm được đường thẳng delta đi qua B(-1;-1)
Hệ số k = tan45 = 1 .
Tự xử nốt