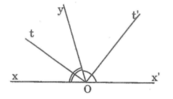
vẽ hai góc kề bù xoy và yox ; biết góc xoy = 1400, gọi ot là tia phân giác của xoy .tính kot
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.


Bạn tự vẽ hình nha ==''
xOy + yOx' = 1800 (2 góc kề bù)
1200 + yOx' = 1800
yOx' = 1800 - 1200
yOx' = 600
Ot là tia phân giác của xOy
=> xOt = tOy = xOy : 2 = 120 : 2 = 600

Ta có yOx' = 180o-110o=70o
Ot là phân giác của xOy =>tOy=xOt=1/2xOy=110o:2=55o
Mà x'Ot=x'Oy+tOy
=>x'Ot=55o+70o=125o
y t x x'
Vì Ot là tia phân giác\(\widehat{xOy}\) của nên \(\widehat{xOt}\)=\(\widehat{yOt}\)=\(\frac{\widehat{xOy}}{2}\)= 55
Vì \(\widehat{xOy}\)và \(\widehat{yOx'}\)là hai góc kề bù nên \(\widehat{xOy}\)+\(\widehat{yOx'}\)=180
110 + \(\widehat{yOx'}\)=180
\(\widehat{yOx'}\)=70
Ta có: \(\widehat{yOx'}\)+ \(\widehat{yOt}\)= \(\widehat{x'Ot}\)
70 + 55 =\(\widehat{x'Ot}\)
\(\widehat{x'Ot}\)= 125

\(xOy+yOx'=180^0\) (2 góc kề bù)
\(110^0+yOx'=180^0\)
\(yOx'=180^0-110^0\)
\(yOx'=70^0\)
Om là tia phân giác của xOy
=> \(xOm=mOy=\frac{xOy}{2}=\frac{110^0}{2}=55^0\)
On là tia phân giác của yOx'
=> \(x'On=nOy=\frac{x'Oy}{2}=\frac{70^0}{2}=35^0\)
\(mOn=nOy+yOm\)
\(mOn=35^0+55^0\)
\(mOn=90^0\)
Chúc bạn học tốt![]()

Trả lời:
góc x'Om= 55+70 =125 độ
góc xOn= 110+35 =145 độ
góc nOm= 35+55= 90 độ
O x y x' m n
Vì 2 góc xoy và yox' là hay góc kề bù
=> Tia Oy nằm giữa 2 tia Ox và Ox'
Ta có :
\(\widehat{xOy}+\widehat{yOx'}=\widehat{xOx'}\)
hay \(110^0+\widehat{yOx'}=180^0\)
\(\Rightarrow\widehat{yOx'}=70^0\)
Vì tia Om là tia phân giác của góc xOy ta có :
\(\widehat{xOm}=\widehat{mOy}=\frac{\widehat{xOy}}{2}=\frac{110^0}{2}=55^0\)
Vì tia On là tia phân giác của góc yOx' ta có :
\(\widehat{yOn}=\widehat{nOx'}=\frac{\widehat{yOx'}}{2}=\frac{70^0}{2}=35^0\)
Trên cùng một nửa mặt phẳng bờ chứa tia xx'
Ta có : \(\widehat{xOm}< \widehat{xOx'}\left(55^0< 180^0\right)\)
=> Tia Om nằm giữa 2 tia Ox và Ox'
Ta có :
\(\widehat{xOm}+\widehat{x'Om}=\widehat{xOx'}\)
hay \(55^0+\widehat{x'Om}=180^0\)
\(\Rightarrow\widehat{x'Om}=125^0\)
Trên cùng một nửa mặt phẳng bờ chứa tia xx'
Ta có : \(\widehat{nOx'}< \widehat{xOx'}\left(35^0< 180^0\right)\)
=> Tia On nằm giữa 2 tia Ox và Ox'
Ta có :
\(\widehat{nOx}+\widehat{nOx'}=\widehat{xOx'}\)
hay \(\widehat{nOx}+35^0=180^0\)
\(\Rightarrow\widehat{nOx}=145^0\)
Trên cùng một nửa mặt phẳng bờ chứa tia xx'
Ta thấy Tia Oy nằm giữa 2 tia Ox và Ox'
hay tia Oy cũng nằm giữa 2 tia Om và On
Ta có :
\(\widehat{mOy}+\widehat{yOn}=\widehat{mOn}\)
hay \(55^0+35^0=\widehat{mOn}\)
\(\Rightarrow\widehat{mOn}=90^0\)
Vậy \(\widehat{x'Om}=125^0;\)\(\widehat{xOn}=145^0\)và \(\widehat{nOm}=90^0\)

Ta có
xOy + x'Oy = 180o (Kề bù)
mà xOy = 80o
=> x'Oy = 100o
Vì Oz là phân giác của x'Oy
=> x'Oz = zOy = \(\frac{1}{2}x'Oy\)= 50o
Số đo góc xOz là
80 + 50 = 130 độ
K cho mk nha

1) Ta có: xOy^ = 3* yOx'^
và xOy^ + yOx'^ = 180o
=> 3* yOx'^ + yOx'^ = 180o
4* yOx'^ = 180o
yOx'^ = 45o
=> xOy^ = 3* yOx'^ = 3* 45o = 135o
Vậy yOx'^ = 45o
xOy^ = 135o
2) Ta có: xOy^ + yOx' = 180o (kề bù)
yOm^ = xOy^ /2
yOn^ = yOx'/2
và \(mOn=yOm+yOn\)
\(\Rightarrow mOn=\frac{xOy}{2}+\frac{yOx'}{2}\)
\(=\frac{xOy+yOx'}{2}\)
\(=\frac{180o}{2}\)
\(=90o\)
Vậy mOn^ = 90o

O x z y
Giải : Ta có : \(\widehat{xOy}+\widehat{yOz}=180^0\)(kề bù)
=> góc yOz = 1800 - góc xOy
=> góc yOz = 1800 - 1300
=> góc yOz = 500
Vậy ...
x O x' y 130 o ?
Vì 2 góc xOy và yOx' là 2 góc kề bù nên :
\(\widehat{xOy}+\widehat{yOx'}=180^0\)
\(130^0+\widehat{yOx'}=180^0\)
\(\widehat{yOx'}=180^0-130^0=50^0\).
bạn viết sai đề rồi
kot=140 độ