Cho 2 vectơ đơn vị thỏa mãn . Hãy xác định
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

Cách 1:
Gọi tọa độ của vectơ \(\overrightarrow a \) là (x; y).
Ta có: \(|\overrightarrow a |\, = \sqrt {{x^2} + {y^2}} \).
Đặt \(\overrightarrow i = \frac{1}{{|\overrightarrow a |}}\;.\overrightarrow a \)
\( \Rightarrow \overrightarrow i = \frac{1}{{\sqrt {{x^2} + {y^2}} }}.(x;y) = \left( {\frac{x}{{\sqrt {{x^2} + {y^2}} }};\frac{y}{{\sqrt {{x^2} + {y^2}} }}} \right)\)
\( \Rightarrow |\overrightarrow i |\, = \sqrt {{{\left( {\frac{x}{{\sqrt {{x^2} + {y^2}} }}} \right)}^2} + {{\left( {\frac{y}{{\sqrt {{x^2} + {y^2}} }}} \right)}^2}} = \sqrt {\frac{{{x^2}}}{{{x^2} + {y^2}}} + \frac{{{y^2}}}{{{x^2} + {y^2}}}} = 1\)
Mặt khác:
\(\overrightarrow i = \frac{1}{{|\overrightarrow a |}}\;.\overrightarrow a = \frac{1}{{\sqrt {{x^2} + {y^2}} }}.\overrightarrow a \) và \(\frac{1}{{\sqrt {{x^2} + {y^2}} }} > 0\) với mọi \(x,y \ne 0\)
Do đó vectơ \(\overrightarrow i \) và \(\overrightarrow a \) cùng hướng.
Vậy \(\frac{1}{{|\overrightarrow a |}}\;\overrightarrow a \) (hay \(\frac{{\overrightarrow a }}{{|\overrightarrow a |}}\)) là một vectơ đơn vị, cùng hướng với vectơ \(\overrightarrow a \).
Cách 2:
Với mọi vectơ \(\overrightarrow a \ne \overrightarrow 0 \), ta có: \(|\overrightarrow a |\; > 0 \Rightarrow k = \frac{1}{{|\overrightarrow a |}} > 0\). Đặt \(\overrightarrow i = \frac{1}{{|\overrightarrow a |}}\;.\overrightarrow a = k.\overrightarrow a \)
\(\begin{array}{l} \Rightarrow |\overrightarrow i |\, = \;|k.\overrightarrow a |\; = \;|k|.|\overrightarrow a |\;\\ \Leftrightarrow \left| {\overrightarrow {\,i} \,} \right| = k.|\overrightarrow a |\; = \frac{1}{{|\overrightarrow a |}}.|\overrightarrow a | = 1\end{array}\)
Mặt khác: \(\overrightarrow i = \frac{1}{{|\overrightarrow a |}}\;.\overrightarrow a = k.\overrightarrow a \) và \(k > 0\)
Do đó vectơ \(\overrightarrow i \) và \(\overrightarrow a \) cùng hướng.
Vậy \(\frac{1}{{|\overrightarrow a |}}\;\overrightarrow a \) (hay \(\frac{{\overrightarrow a }}{{|\overrightarrow a |}}\)) là một vectơ đơn vị, cùng hướng với vectơ \(\overrightarrow a \).

Theo giả thiết, ta có 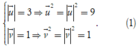
Từ
u
→
-
v
→
=
4
, suy ra ![]()
Kết hợp (1) và (2) ta được ![]()
Khi đó ![]()
Vậym | u → + v → | = 2
Chọn B.

Tham khảo:
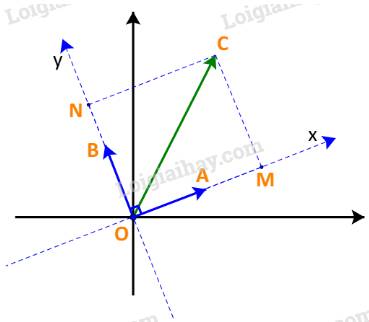
a) Trên mặt phẳng tọa độ, lấy các điểm A, B, C sao cho \(\overrightarrow {OA} = \overrightarrow a ;\;\overrightarrow {OB} = \overrightarrow b ;\;\overrightarrow {OC} = \overrightarrow u \)
Trên hệ trục Oxy với các vectơ đơn vị \(\overrightarrow i = \overrightarrow a ,\;\overrightarrow j = \overrightarrow b \), lấy M, N là hình chiếu của C trên Ox, Oy.
Gọi tọa độ của \(\overrightarrow u \)là \(\left( {x;y} \right)\). Đặt \(\alpha = \left( {\overrightarrow u ,\overrightarrow a } \right)\).
+) Nếu \({0^o} < \alpha < {90^o}\): \(x = OM = \;|\overrightarrow u |.\cos \alpha = \;|\overrightarrow u |.\cos \alpha .\;|\overrightarrow a |\; = \overrightarrow u \,.\,\overrightarrow a \,;\)
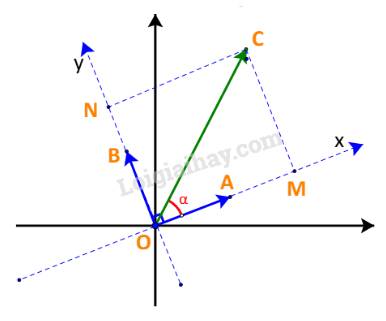
+) Nếu \({90^o} < \alpha < {180^o}\): \(x = - OM = \; - |\overrightarrow u |.\cos ({180^o} - \alpha ) = \;|\overrightarrow u |.\cos \alpha \; = \overrightarrow u \,.\,\overrightarrow a \,;\)

Như vậy ta luôn có: \(x = \overrightarrow u .\overrightarrow a \)
Chứng minh tương tự, ta có: \(y = \overrightarrow u .\overrightarrow b \)
Vậy vectơ \(\overrightarrow u \) có tọa độ là \((\overrightarrow u \,.\,\overrightarrow a \,;\,\overrightarrow u \,.\,\overrightarrow b )\)
b) Trong hệ trục Oxy với các vectơ vectơ đơn vị \(\overrightarrow i = \overrightarrow a ,\;\overrightarrow j = \overrightarrow b \), vectơ \(\overrightarrow u \) có tọa độ là \((\overrightarrow u \,.\,\overrightarrow a \,;\,\overrightarrow u \,.\,\overrightarrow b )\)
\(\begin{array}{l} \Rightarrow \overrightarrow u = (\overrightarrow u \,.\,\overrightarrow a \,).\overrightarrow i + (\,\overrightarrow u \,.\,\overrightarrow b ).\overrightarrow j \\ \Leftrightarrow \overrightarrow u = (\overrightarrow u \,.\,\overrightarrow a \,).\overrightarrow a + (\,\overrightarrow u \,.\,\overrightarrow b ).\overrightarrow b \end{array}\)

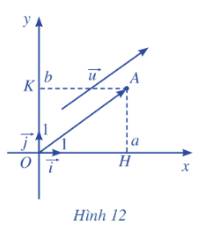
a) Do \(\overrightarrow {OA} {\rm{ }} = {\rm{ }}\overrightarrow u \) nên tọa độ vecto \(\overrightarrow {OA} = \left( {a;b} \right)\). Vậy tọa độ điểm A là: \(A\left( {a;b} \right)\)
b) TỌa độ điểm H là \(H\left( {a;0} \right)\) nên \(\overrightarrow {OH} = \left( {a;0} \right)\). Do đó, \(\overrightarrow {OH} = a\overrightarrow i \)
c) TỌa độ điểm K là \(K\left( {0;b} \right)\) nên \(\overrightarrow {OK} = \left( {0;b} \right)\). Do đó, \(\overrightarrow {OK} = b\overrightarrow j \)
d) Ta có: \({\rm{ }}\overrightarrow u = \overrightarrow {OA} {\rm{ }} = \overrightarrow {OH} + \overrightarrow {OK} = a\overrightarrow i + b\overrightarrow j \) (đpcm)

a) Ta có: \({\overrightarrow i ^2} = {\left| {\overrightarrow i } \right|^2} = 1;{\overrightarrow j ^2} = {\left| {\overrightarrow j } \right|^2};\overrightarrow i .\overrightarrow j = 0\)(vì \(\overrightarrow i \bot \overrightarrow j \) )
b) Ta có: \(\overrightarrow u .\overrightarrow v = \left( {{x_1}\overrightarrow i + {y_1}\overrightarrow j } \right).\left( {{x_2}\overrightarrow i + {y_2}\overrightarrow j } \right) = {x_1}{x_2}.{\overrightarrow i ^2} + {x_1}{y_2}.\left( {\overrightarrow i .\overrightarrow j } \right) + {y_1}{x_2}.\left( {\overrightarrow j .\overrightarrow i } \right) + {y_1}{y_2}.{\overrightarrow j ^2} = {x_1}{x_2} + {y_1}{y_2}\)


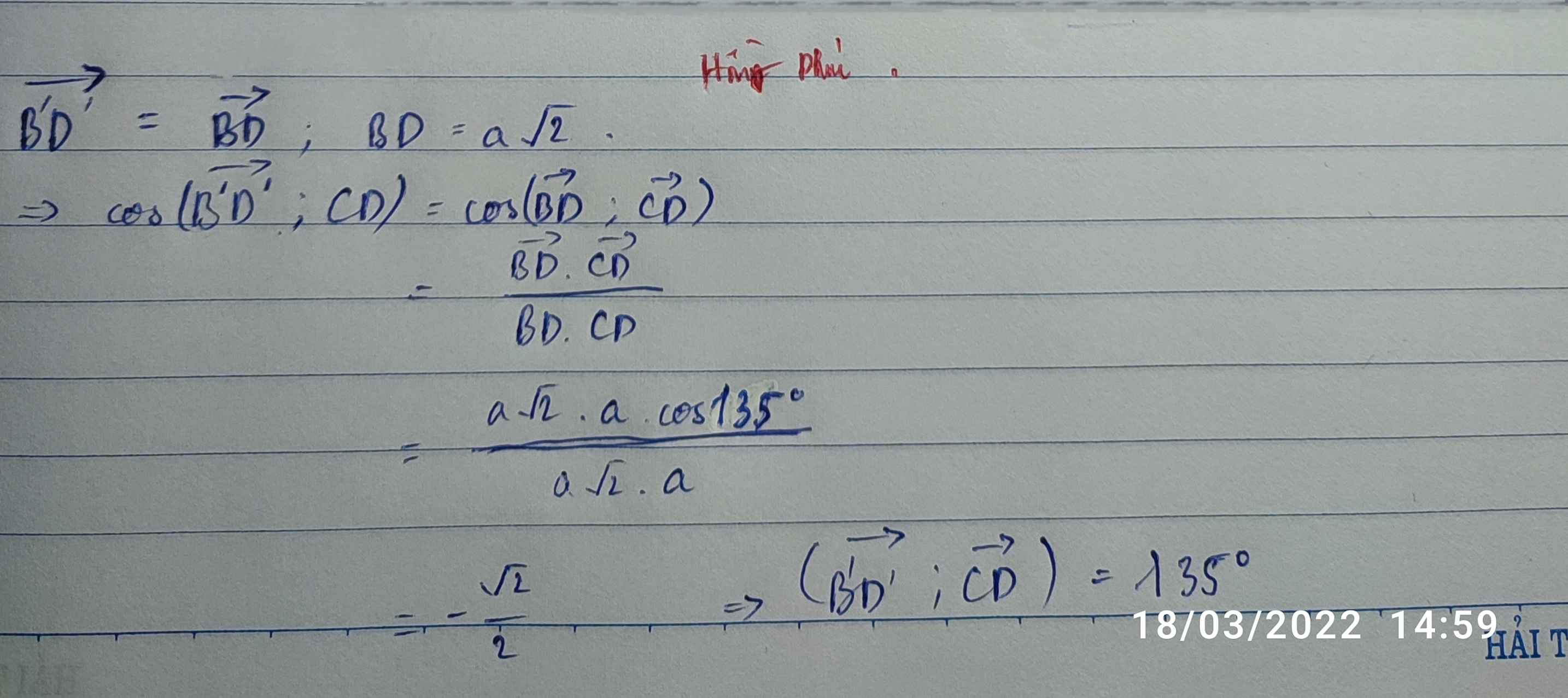
Chọn D.
Do 2 vecto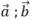 là 2 vecto đơn vị nên độ dài mỗi vecto là 1.
là 2 vecto đơn vị nên độ dài mỗi vecto là 1.
Suy ra:
= 6.1- 20.1+ 7.1= - 7.