cho a-2=x+y
CM; ax+2x+ay+2y+4=a^2
K
Khách
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.
Những câu hỏi liên quan
NT
1
22 tháng 7 2019
Ta có: 2yz + y2 + z2 - x2
= (y2 + 2yz + z2) - x2
= (y + z)2 - x2
= (y + z + x)(y + z - x)
= 2a(y + z + x - 2x)
= 2a(2a - 2x)
= 2a.2(a - x)
= 4a(a - x) --> Đpcm
T
2
DV
2
T
13 tháng 9 2018
a) Ta có \(\left(a-b\right)^2\ge0\)
\(\Leftrightarrow a^2-2ab+b^2\ge0\)
\(\Leftrightarrow a^2+b^2\ge2ab\)
\(\Leftrightarrow\frac{a^2+b^2}{2}\ge ab\)( chia 2 vế cho 2 )
b) \(\frac{a+1}{a}\)chưa lớn hơn hoặc bằng 2 đc , bạn thay a=2 vào thì 3/2<2
c) Ta có \(x^2\ge0\);\(y^2\ge0\);\(z^2\ge0\)
nên \(x^2+y^2+z^2\ge0\)
\(\Rightarrow x^2+y^2+z^2+3\ge3\)
13 tháng 9 2018
Ta có \(\left(a-b\right)^2\ge0\)
\(\Leftrightarrow a^2-2ab+b^2\ge0\)
\(\Leftrightarrow a^2-2ab+b^2\ge0\)
\(\Leftrightarrow a^2+b^2\ge2ab\Leftrightarrow\frac{a^2+b^2}{2}\ge ab\)
13 tháng 4 2023
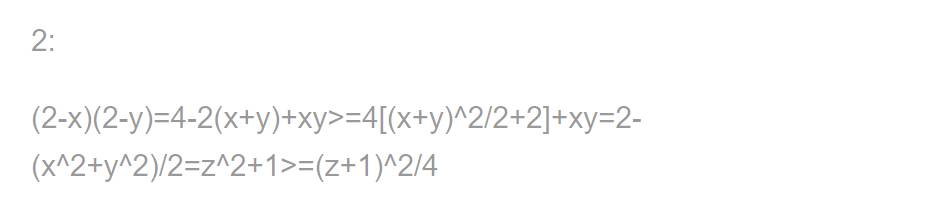
Tương tự, ta được:
\(\left(2-y\right)\left(2-z\right)>=\dfrac{\left(x+1\right)^2}{4}\)
và \(\left(2-z\right)\left(2-x\right)>=\left(\dfrac{y+1}{2}\right)^2\)
=>8(2-x)(2-y)(2-z)>=(x+1)(y+1)(z+1)
(x+yz)(y+zx)<=(x+y+yz+xz)^2/4=(x+y)^2*(z+1)^2/4<=(x^2+y^2)(z+1)^2/4
Tương tự, ta cũng co:
\(\left(y+xz\right)\left(z+y\right)< =\dfrac{\left(y^2+z^2\right)\left(x+1\right)^2}{2}\)
và \(\left(z+xy\right)\left(x+yz\right)< =\dfrac{\left(z^2+x^2\right)\left(y+1\right)^2}{2}\)
Do đó, ta được:
\(\left(x+yz\right)\left(y+zx\right)\left(z+xy\right)< =\left(x+1\right)\left(y+1\right)\left(z+1\right)\)
=>ĐPCM
R
1
6 tháng 9 2018
\(\left(a^2+b^2\right)\left(x^2+y^2\right)=\left(ax+by\right)^2\)
\(\Rightarrow a^2x^2+a^2y^2+b^2x^2+b^2y^2=a^2x^2+2axby+b^2y^2\)
\(\Rightarrow a^2y^2+b^2x^2=2axby\)
\(\Rightarrow a^2y^2-2axby+b^2x^2=0\)
\(\Rightarrow\left(ay\right)^2-2.ay.bx+\left(bx\right)^2=0\)
\(\Rightarrow\left(ay-bx\right)^2=0\)
\(\Rightarrow ay-bx=0\Rightarrow ay=bx\Rightarrow\frac{a}{x}=\frac{b}{y}\)
\(VT=ax+2x+ay+2y+4\)
\(=a\left(x+y\right)+2\left(x+y\right)+4\)
\(=a\left(a-2\right)+2\left(a-2\right)+4\)
\(=a^2-2a+2a-4+4=a^2=VP\)
Ta có: \(VT=ax+2x+ay+2y+4\)
\(=\left(c+y\right)a+2\left(x+y\right)+4\)
\(=\left(a+2\right)\left(x+y\right)+4\)
mà \(a-2=x+y\)
\(\Rightarrow VT=\left(a+2\right)\left(a-2\right)=a^2-4+4=a^2\)
\(\Leftrightarrow VP\) -> ĐPCM.