1, Có 4 điện trở R1 = 10 R2 = 10 ; R3 = 30 R4 = 40
a, Dùng 3 điện trở R1 ; R2 ; R3 có thể mắc thành bao nhiêu mạch điện khác nhau?.Tính điện trở tương đương của mỗi mạch điện đó.
b, Hãy tìm cách mắc cả 4 điện trở thành mạch điện có điện trở 16 ôm. Vẽ sơ đồ cách mắc đó.
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

\(R_{23}=\dfrac{R_2.R_3}{R_2+R_3}=\dfrac{10.15}{10+15}=6\left(\Omega\right)\)
\(R_{tđ}=R_1+R_{23}=9+6=15\left(\Omega\right)\)
\(I=I_1=I_{23}=\dfrac{U}{R_{tđ}}=\dfrac{27}{15}=1,8\left(A\right)\)
\(U_{23}=U_2=U_3=I_{23}.R_{23}=1,8.6=10,8\left(V\right)\)
\(\left\{{}\begin{matrix}I_2=\dfrac{U_2}{R_2}=\dfrac{10,8}{10}=1,08\left(A\right)\\I_3=\dfrac{U_3}{R_3}=\dfrac{10,8}{15}=0,72\left(A\right)\end{matrix}\right.\)
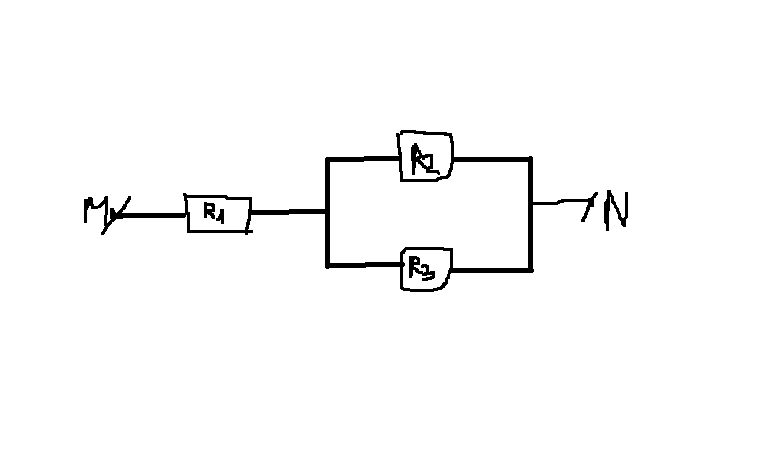
\(R_{23}=\dfrac{R_2\cdot R_3}{R_2+R_3}=\dfrac{10\cdot15}{10+15}=6\Omega\)
\(R_m=R_1+R_{23}=R_1+\dfrac{R_2R_3}{R_2\cdot R_3}=9+\dfrac{10\cdot15}{10+15}=15\Omega\)
\(I_1=I_{23}=I_m=\dfrac{U}{R}=\dfrac{27}{15}=1,8A\)
\(U_2=U_3=U_{23}=I_{23}\cdot R_{23}=6\cdot1,8=10,8V\)
\(\Rightarrow\) \(I_2=\dfrac{U_2}{R_2}=\dfrac{10,8}{10}=1,08A\)
\(I_3=\dfrac{U_3}{R_3}=\dfrac{10,8}{15}=0,72A\)

\(R_{tđ}=R_1+R_2+R_3=4+10+35=49\left(\Omega\right)\)
\(I=I_1=I_2=I_3=\dfrac{U_3}{R_3}=\dfrac{7,5}{35}=\dfrac{3}{14}\left(A\right)\)
\(\left\{{}\begin{matrix}U_1=I_1.R_1=\dfrac{3}{14}.4=\dfrac{6}{7}\left(V\right)\\U_2=I_2.R_2=\dfrac{3}{14}.10=\dfrac{15}{7}\left(V\right)\\U_m=I.R_{tđ}=\dfrac{3}{14}.49=\dfrac{21}{2}\left(V\right)\end{matrix}\right.\)

Cho ba điện trở R1 = R2 = 10 , R3 = 20 . R1 mắc song R2, R1 và R2 mắc nối tiếp với R3. Điện trở tương đương của đoạn mạch là: A. 10Ω B.15Ω C.20Ω D.25Ω
Giải thích:
\(R_3nt\left(R_1//R_2\right)\)
\(R_{12}=\dfrac{R_1\cdot R_2}{R_1+R_2}=\dfrac{10\cdot10}{10+10}=5\Omega\)
\(R_{tđ}=R_3+R_{12}=20+5=25\Omega\)
Chọn D.

đáp án D
R = R 1 + R 2 + R 3 = 12 Ω ⇒ I = ξ R + r = 24 12 + 0 = 2 A A n g = ξ I t = 12 . 2 . 10 . 60 = 14400 J P R 2 = I 2 R 2 = 2 2 . 4 = 16 W

CTM: \(R_1nt\left(R_2//R_b\right)\)
+\(R_b=0\):
\(R_2//R_b\Rightarrow\)\(R_{2b}=\dfrac{R_2\cdot R_b}{R_2+R_b}=\dfrac{10\cdot0}{10+0}=0\)
\(R_{tđ}=R_1+R_{2b}=15+0=15\Omega\)
Như vậy, dòng điện qua \(R_1\) max\(\Leftrightarrow I_{1min}=\dfrac{U}{R_{tđ}}=\dfrac{4,5}{15}=0,3A\)
+\(R_b=30\Omega:\)
\(R_{2b}=\dfrac{R_2\cdot R_b}{R_2+R_b}=\dfrac{10\cdot30}{10+30}=7,5\Omega\)
\(R_{tđ}=R_1+R_{2b}=15+7,5=22,5\Omega\)
Lúc này, dòng điện qua \(R_1\) min\(\Leftrightarrow I_{1max}=\dfrac{U}{R_{tđ}}=\dfrac{4,5}{22,5}=0,2A\)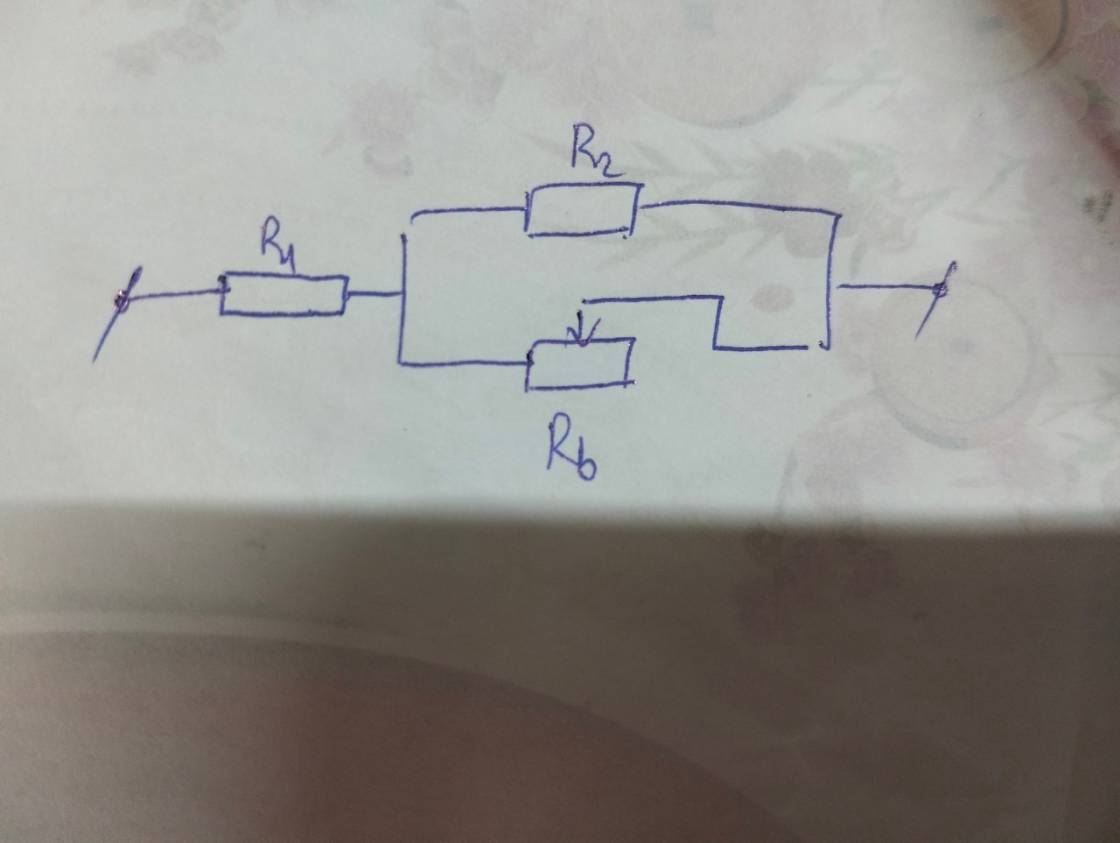

Vì Rtđ >R1(16>10)
nên MCD R1nt R2
Điện trở R2 là
\(R_2=R_{tđ}-R_1=16-10=6\left(\Omega\right)\)

a) Để tính số mạch điện khác nhau có thể mắc từ 3 điện trở R1, R2, R3, ta sử dụng công thức tính số cách kết hợp chập k của n phần tử. Trong trường hợp này, chúng ta có n = 3 và k = 3.
Số mạch điện khác nhau = C(3, 3) = 1
Vậy có 1 mạch điện khác nhau có thể mắc từ 3 điện trở R1, R2, R3.
Điện trở tương đương của mạch điện này là R1 + R2 + R3 = 10 + 10 + 30 = 50 Ω.
b) Để mắc cả 4 điện trở thành mạch điện có điện trở 16 Ω, chúng ta có thể sử dụng mạch nối tiếp và song song.
Cách mắc như sau:
Đặt R1 và R2 nối tiếp nhau: R12 = R1 + R2 = 10 + 10 = 20 ΩR3 nối song song với R12: R123 = 1/(1/R12 + 1/R3) = 1/(1/20 + 1/30) = 12 ΩR4 nối tiếp với R123: R1234 = R123 + R4 = 12 + 40 = 52 ΩTa có R1234 = 16 Ω, vậy cách mắc này đạt yêu cầu.
Sơ đồ mạch điện:
---[R1]---[R2]--- | | ---[R3]---[R4]---Trong sơ đồ trên, dấu --- biểu thị mạch nối tiếp và dấu | biểu thị mạch song song.