Cho ΔPQR cân tại P có PQ = 13cm; QR = 24cm. Kẻ phân giác trong PM (M ∈ PM). Gọi O là trung điểm của PQ và K là điểm đối xứng của M qua O.
a) Tính diện tích tam giác PQR.
b) Tứ giác PMQK là hình gì? Vì sao?
c) Để tứ giác PMQK là hình vuông thì tam giác PQR phải có thêm điều kiện gì?
d) So sánh diện tích tam giác ABC với diện tích tứ giác PKQM.

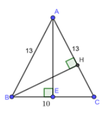
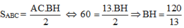

a: MQ=MR=QR/2=12cm
=>PM=5cm
\(S=\dfrac{5\cdot24}{2}=5\cdot12=60\left(cm^2\right)\)
b: Xét tứ giác PMQK có
O là trung điểm chung của PQ và MK
góc PMQ=90 độ
Do đó: PMQK là hình chữ nhật
c: Để PMQK là hình vuông thì PM=MQ=QR/2
=>ΔPQR vuông tại P
=>góc QPR=90 độ